
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Vectors and scalars
A change of position of a particle is called a displacement. A displacement is characterized by a length and a direction. We can represent a subsequent displacement from A to B and C, fig.1.2. The net effect of the two displacements will be the same as a displacement from A to C. We speak then of AC as the sum or resultant of the displacements AB and BC. Notice that this sum is not an algebraic sum and that a number alone cannot uniquely specify it. Quantities that behave like displacements are called vectors. Vectors, than, are quantities that have both magnitude and direction and combine according to certain rules of addition.

Figure 1.2
Quantities that can be completely specified by a number and unit and that therefore have magnitude only are called scalars.
To represent a vector on a diagram we draw an arrow. The relation among vectors 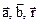 can be written as
can be written as
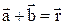 . (1.2)
. (1.2)
Another way of adding vectors is the analytical method, involving the resolution of a vector into component with respect to a particular coordinate system. Fig.1.2. shows a vector 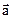 whose tail has been placed at the origin of a rectangular coordinate system. If we drop perpendicular lines from the head of
whose tail has been placed at the origin of a rectangular coordinate system. If we drop perpendicular lines from the head of 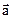 to the axis the quantities
to the axis the quantities 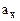 and
and 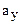 so formed are called the components of the vector
so formed are called the components of the vector 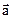 .
.
The process is called resolving 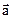 vector into its components. The components
vector into its components. The components 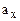 and
and 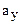 are found readily from
are found readily from
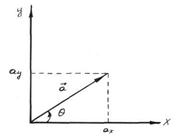
Figure 1.3
 (1.3)
(1.3)
where 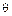 is the angle that the vector
is the angle that the vector 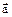 makes with the positive x-axis, measured counter-clockwise from this axis. To obtain
makes with the positive x-axis, measured counter-clockwise from this axis. To obtain  and
and 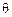 from
from 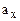 and
and 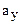
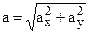 and
and  . (1.4)
. (1.4)
When we multiply a vector quantity by another vector quantity by another vector quantity, we must distinguish between the scalar product and the vector product. The scalar product of two vectors 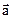 and
and  , written as
, written as  , is defined to be
, is defined to be
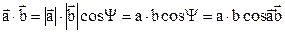 , (1.5)
, (1.5)
where 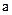 is the magnitude of vector
is the magnitude of vector 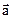 ,
, 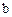 is the magnitude of vector
is the magnitude of vector  , and
, and 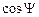 is the cosine of the angle
is the cosine of the angle 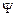 between the two vectors.
between the two vectors.
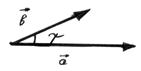
Figure 1.4
The notation  is also called the dot product of
is also called the dot product of 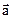 and
and  and is spoken as “
and is spoken as “ 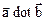 ”. The vector product of two vectors
”. The vector product of two vectors 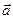 and
and 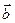 is written as
is written as 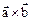 and is vector
and is vector  , where
, where
 . (1.6)
. (1.6)
The magnitude of  is defined by
is defined by
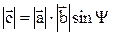 , (1.7)
, (1.7)
where 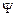 is the angle between
is the angle between 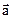 and
and  .
.
The direction of 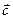 , the vector product of
, the vector product of 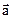 and
and 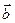 , is defined to be perpendicular to the plane formed by
, is defined to be perpendicular to the plane formed by 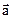 and
and  .
.
Imagine rotating a right – handed screw whose axis is perpendicular to the plane formed by 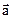 and
and  so as to turn it from
so as to turn it from 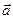 to
to  through the angle
through the angle 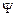 between them. Another convenient way to obtain the direction of a vector product is the following. Imagine an axis perpendicular to the plane of
between them. Another convenient way to obtain the direction of a vector product is the following. Imagine an axis perpendicular to the plane of 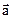 and
and  through their origin. Now wrap the fingers of the right hand around this axis and push the vector
through their origin. Now wrap the fingers of the right hand around this axis and push the vector 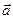 into the vector
into the vector  through the smaller angle between them with the fingertips, keeping the thumb erect;
through the smaller angle between them with the fingertips, keeping the thumb erect;
The notation, 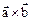 is also called the cross product of
is also called the cross product of 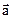 and
and  and spoken as “
and spoken as “ 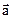 cross
cross  ”.
”.
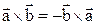 . (1.8)
. (1.8)

Figure 1.5
We are starting the study of physics today. Until the beginning of the seventeenth century mankind had little understanding of the structure of the material world. Man believed that stones were stones, fire was fire, and water was simply water. Now we know that all kinds of substances consist of very small invisible particles - atoms. They make up all the elements and compounds that exist in the world. Their interactions provide the energy that man uses.
In the nineteenth century the scientists first established experimentally the atomic theory of the structure of a matter. They found that the simple forms of a matter were chemical elements which consisted of atoms – indivisible particles of very small size.
At the end of the nineteenth century scientists achieved a great quantity of information on the atomic structure of a matter and the general nature of the atom, which, they found, was further divisible. They discovered most of the chemical elements and found that atoms of each element were different in chemical and physical properties from properties of other elements. A further discovery showed that the atoms combine in small numbers and form units of matter or molecules and that in all substances the atoms and molecules are in a state of rapid motion.
When we think of the substance which we call water, we commonly think of it as a definite liquid. It does not mean, however, that it is the only possible state in which water can exist. The liquid state is the normal state for the substance which we call water, but water can exist also as a gas and as a solid; in the gaseous state it changes to steam or water vapour, and in the solid state it becomes ice. Many substance can and do at various times exist in more than one of these three possible states. The molecules move differently in the three states.
In gases we find that the gas molecules are free to move and they are quite far apart. A body of gas no definite volume or shape, but takes the volume and shape of the vessel. A solid has both volume and shape. The molecules of a solid are also in motion, but they can move only a small amount because the atoms are very close together. The closer the molecules are together, the less free they are to move. The liquid state is between the gaseous and solid states. The molecules of a liquid are less free of move than the gas molecules, but are freer to move than the molecules of a solid.
The molecules of a solid are very close together and have a great attraction for each other. The closer they are together, the heavier is the solid; however, the molecules are in a state of continual vibration. In this state their attraction for each other is very great, and that is why it is very difficult to change the shape of a solid.
It we heat the solid, the molecules begin to vibrate more and more and three fore there is less attraction for each other. Thus, a solid expands when we heat it. When the molecules are quite far apart from each other, the solid changes into a liquid.
The story of mans civilization is the story of his study of nature. The scientific method of studying of nature. Those, who apply the principles of physics are called “engineers”. Physics and mathematics are the basic “foundations of engineering”. When you can measure what you are speaking about, and express it in numbers, you know something about it.
Lecture 2. Kinematics
Mechanics study the motion of objects and the forces that affect their motion. When a body changes its position relative to other bodies. It is said to be in mechanical motion.
The classic mechanics was founded in sixteenth and seventeenth centuries due to the work of Galileo Galilei and Isaac Newton. Mechanics is divided into three branches: kinematics, dynamics and static’s. Kinematics deals with motion without considering its cause. Dynamics considers laws of motion and the factors, which cause this motion. Static deals with laws of equilibrium of body. We shall begin our studies with the motion of a particle.
Kinematics studies the motion of a material point or bodies without regard to the courses of this motion. The basic concepts of kinematics are following: the material point; the frame of reference; the radius-vector; the trajectory; the path length; the displacement; the velocity; the acceleration.
If the dimensions and the shape of a body are not considered in a particular phenomenon, we can conceive a body as being represented by a point. A material point is a body dimensions of which may be neglected within a given problem.
In order to describe the motion of a particle, one must indicate which points in space the particle has passed and the points in time during which it was located in one or another point of the path. The location of the point in a coordinate system is determined by three coordinates x, y, z, or by radius vector 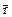 , drawn from the origin of the coordinate system to the given point. The radius vector
, drawn from the origin of the coordinate system to the given point. The radius vector 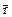 is given by the magnitude
is given by the magnitude
 , (2.1)
, (2.1)
and the angles it forms with the coordinate axes
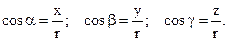 (2.2)
(2.2)
Frame of reference is a body reference, system of axes closely connected with it and clock. Body of reference is any body referring to which positions of other objects are determined. In order to describe the motion of a body we must first select a frame of reference, i.e., we choose one or several bodies considered to be fixed, and construct a coordinate system, say, a rectangular one (fig. 2.1).
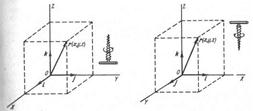
Figure 2.1
A change in position respectively to a frame of reference is called motion of a body. Mechanics, the oldest of the physical sciences, is the study of the motion of objects. When we describe motion we deal with the part of mechanics called kinematics. Thus, the motion in space can be described in the form of a continuous function
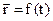
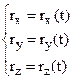 . (2.3)
. (2.3)
Its vector equation is called the equation of motion. Let us consider AB, a portion of the path. Assume that at the instant of time t the moving particle was at A, and at the instant of time 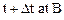 .
.
Let us introduce the radius vectors 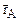 and
and 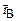 . We know that during the interval of time
. We know that during the interval of time  , the particle moved from A to B. It is therefore natural to call the vector AB the particle displacement vector.
, the particle moved from A to B. It is therefore natural to call the vector AB the particle displacement vector.
The curvilinear motion is determined by the displacement vector  for time
for time 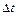 , where the smaller
, where the smaller  is the greater is the accuracy. The motion of a body may be:
is the greater is the accuracy. The motion of a body may be:
- translational, if any straight line that passes through the body remains continually parallel to itself, and
- rotational, if the points of a body create concentric circles.
Velocity
To characterize the rapidity of motion used the term of velocity. The average speed for the path AB is given by the relation
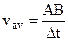 . (2.4)
. (2.4)

Figure 2.2
The velocity of a particle is the rate at which its position changes with time.
 . (2.5)
. (2.5)
As 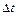 decreases, the ratio
decreases, the ratio 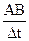 approaches a limit. The vector
approaches a limit. The vector  having the direction of the tangent to the curve at the given moment limit of the ratio
having the direction of the tangent to the curve at the given moment limit of the ratio 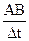 as
as 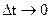 , is called the instantaneous particle velocity
, is called the instantaneous particle velocity
 . (2.6)
. (2.6)
Let us now consider the curvilinear path AB, (fig.2.2) vectors 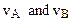 differ in magnitude as well as in direction. To determine the increase in magnitude with the velocity, it is necessary, as before, to subtract the magnitude of the vector
differ in magnitude as well as in direction. To determine the increase in magnitude with the velocity, it is necessary, as before, to subtract the magnitude of the vector 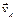 from the magnitude of the vector
from the magnitude of the vector 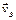 :
:
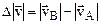 . (2.7)
. (2.7)
Vector v is directed along the tangent to the trajectory in the direction of motion. The unit of velocity is m/s. Vector v can be resolved in to the axis:
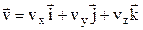 . (2.8)
. (2.8)
Modulus of vector 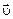 can be expressed as:
can be expressed as:
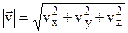 ; (2.9)
; (2.9)
where 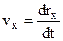 ;
;  ;
; 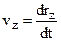 .
.
Date: 2015-01-12; view: 1373
| <== previous page | | | next page ==> |
| Measurement | | | Ultimate velocity |