SYSTEM OF CELESTIAL COORDINATES

I. It is known that the position of any point on Earth surface is determined by geographic latitude j and longitude l.

Celestial coordinates determine the position of celestial bodies on the celestial sphere. They are similar to geographic coordinates; however in astronomy several systems of coordinates are used. Let's get acquainted with two of them.

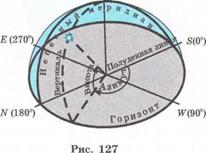
II. Horizontal coordinate system. The apparent position of stars on the sky relative the horizon and points of the horizon is easily determined in the horizontal coordinate system (fig. 127). In this system the fundamental plane is the plane of the observer’s local horizon. The position of a star is determined by two angles: one of them measured along the horizon up to vertical of the star is called azimuth A of the star. Note that in astronomy azimuths are measured from the South to the West while in geography they are measured from the North to the East. The second angle is the altitude h of a star above the horizon. It is measured from the horizon along the vertical up to the star. Altitude of the star is an angle between -90° to +90°. Using the measuring devices (for example, a theodolit) it is very easy to determine horizontal coordinates of a celestial body.

However this system of coordinates has some inconveniences. Horizontal coordinates of celestial bodies depend on the location of the observer, the time of day and date. Therefore it is impossible to use these coordinates for drawing up celestial maps and atlases. Horizontal coordinates are used to specify the position of a star in the sky from a certain place at a given time.

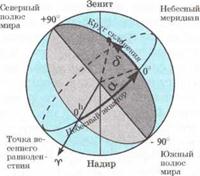
III. Equatorial coordinate system. As the celestial sphere rotates as a whole and the relative location of stars and constellations doesn't change then it is convenient to use the system of coordinates which rotates together with the celestial sphere. That is the equatorial coordinate system (fig. 128). The fundamental plane of this system is the plane of the celestial equator. The coordinates of this system are declination d and right ascension a. Declination of a star like geographic latitude is measured by an arch from the celestial equator along a celestial meridian up to a star. Declination is measured in degrees from 0^o to +90 ° (for the stars which are in the Northern hemisphere) and from 0^o to -90° (for the stars which are in the Southern hemisphere).

The right ascension of a star like the geographic longitude is measured by an arch from the Vernal equinox ( 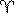) along the celestial equator towards to the apparent daily rotation of the celestial sphere up to the celestial meridian. It is measured in degrees (from 0^о to 360^o) but more often in hours (from 0 to 24^h) *. As the complete revolution of the celestial sphere occurs in 24h, it is easy to verify that 1^h = 15°, 1^m = 15', 1^s =15" and vice versa: 1° = 4^h, 1' = 4^s.

The equatorial coordinates of stars don't depend on the location of an observer and don't change throughout a long time. These coordinates are used to map the stars and register them in catalogs.

Fig.128

Self-testing questions

1. What horizontal coordinates of stars do you know?

2. Why it is impossible to use horizontal coordinate system for mapping stars?

3. What are the azimuths of four points of the celestial horizon?

4. What equatorial coordinates of stars are known to you?

5. Relative what elements of the celestial sphere are measured the equatorial coordinates?

6. Do the equatorial coordinates of a star change within a day?

7. What is the declination of a star if it is on the celestial equator?

^* In astronomy the following designations are used: hour-1^h, minute-1^m, second-1^s

Exercise 31

1. The angular distance between the Polaris and Sirius is 106^o. Positive or negative is the declination of the Sirius?

2. Express in degrees: a) 6^h 24^m; b) 18^h 43^m.

3. Express in hours: a) 90^o30'; b) 105^o 43'.

4. Determine in what hemisphere, Northern or Southern, is located each of the stars given in the table 9.

Date: 2015-01-12; view: 1779