When 8is sufficiently small, the first term is the smaller of the two, and it is well approximated by the expression 2 page

To analyze this problem, consider the following "marriage game." There are two classes of agents—say men and women—who can enter into partnerships or "marriages" with one another. Each marriage is governed by one of three types of contractual arrangements: the man controls, the woman controls, or they share control. Let us assume that each of these arrangements is equally efficient, so that the only issue is the distribution of power in the relationship. Let us further assume that the likelihood that an individual enters into a given contractual arrangement is influenced by the degree to which that arrangement is customary in the given society.

The evolutionary process operates as follows. In each period, one man and one woman are tentatively matched, and each proposes one of the three possible contracts. If they name the same contract they get married; if they name different ones they break up. Suppose the payoffs are as follows:

The Marriage Game

Men

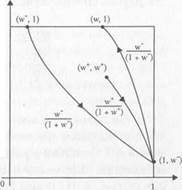
The fact that each outcome has the same total utility is not significant here; indeed the utility functions can be re-scaled in any way that we wish without affecting the resistances between the three coordination equilibria (see equation (9.5)). These resistances are illustrated in Fig­ure 9.2. From this we see that the sharing norm is the unique stochas­tically stable outcome whenever the sample size is sufficiently large. Concretely this means that, when the noise is small, the sharing norm will be observed with substantially higher probability over the long run than will either of the other arrangements.

It is important to recognize that this result depends on the welfare im­plications of the various contractual arrangements, not on their specific terms. In particular, the model does not necessarily predict equal treat­ment in situations where the parties have unequal abilities or tastes. In this case, efficiency might well call for asymmetric arrangements in which each partner takes on those tasks to which he or she is particularly inclined or particularly well-suited. The general point of theorem 9.1 is that there is a long-run selection bias toward contractual arrangements that offer both sides a fairly high level of welfare relative to the welfare they could enjoy under alternative arrangements.

Moreover, there is a simple intuitive explanation for this result. Con­ventions with extreme payoff implications are relatively easy to dislodge because the members of one of the groups are dissatisfied compared to what they could get under some other arrangement. It does not take many stochastic shocks to create an environment in which members of the dissatisfied group prefer to try something different. This involves a risk of being "unattached," but if the payoffs from being attached are sufficiently meager, it may be a risk worth taking. Under the sharing norm, by contrast, both sides enjoy reasonably high payoffs given their

Figure 9.2. Reduced resistances between equilibria in the marriage game.

alternatives; hence there is less impetus for change. More generally, theorem 9.1 says that the evolutionary process tends over time to push society away from the boundaries of the feasible payoff set, and move it toward the "middle" of the efficiency frontier, as defined by the maximin criterion.

9.5 Examples Showing Departures from Strict Efficiency and Exact Maximin

We now show why the theorem cannot be substantially strengthened. First, we exhibit a situation where the (stochastically) stable contract is efficient but not strictly so. In Figure 9.3, contract 1 weakly Pareto- dominates contract 2, but the least resistant 1-tree (left panel) and the least resistant 2-tree (right panel) have the same resistance. Hence both contracts are stable.

The next example shows that the bound in the theorem is tight when there are at least four games. Choose real numbers zv~, zv, and zv⁺ such

© lA

Row payoff 0 Row payoff

Figure 9.3. Left: Least resistant 1-tree. Right: Least resistant 2-tree.

Figure 9.4. Left: Least resistant (iv⁺. ttf⁺)-tree. Right: Least resistant (w, 1 )-tree.

that

w < w⁺ < 1.

Consider four contracts with the payoffs shown in Figure 9.4, where u>~ and iv⁺ have the meanings defined in (9.2) and (9.3). The left panel shows the least resistant tree rooted at (w⁺, w⁺); the right panel shows the least resistant tree rooted at (и/. 1). The contract with payoffs (w, 1) has the same or lower stochastic potential than the maximin contract
(и>⁺, w⁺) if

W W⁺ W W~ U> W~

1 + IV~ 1 -I- W⁺ 1 + W~ ~ 1 -I- W~ ⁺ 1 + IV ⁺ W~ + W⁺ '

This reduces to w > (w⁺ - or)/(l + a), where a is defined as in (9.4). Hence the bound in theorem 9.1 is best possible when the game is 4 x 4, and the argument extends naturally to larger games.

9.6 Small Games and Symmetric Coordination Games

In this section we discuss two special classes of games where there is no distortion in the selection process, and the maximin outcome is stochas­tically stable. One such class consists of 2 x 2 coordination games, where the payoffs take the form

From theorem 4.1 we know that adaptive learning selects the equilib­ria that maximize the product of the players' expected payoffs, that is, the risk dominant equilibria. We claim that any such equilibrium is maximin. Let us assume that (1.1) risk dominates (2.2), that is, "i^i > a₂b₂. 'f (1/ 1) also Pareto dominates (2, 2), then (1,1) has wel­fare index wi = л b\/b\ = 1 whereas (2,2) has welfare index w₂ = ciz/n\ лЬ₂/Ь\ < 1. Hence the former is the maximin equilibrium. If (1.1) does not Pareto dominate (2, 2), we may suppose that я, < a₂ and b\ > b₂. Thus the welfare index of (1.1) is W\ = ci\/a₂ л b\/b\ = 0]/a₂, whereas the welfare index of (2.2) is w₂ = a₂/a₂ л b₂/b\ — b₂/b\. Since > b₂/bi, equilibrium (1,1) is maximin.

Next, consider the case of a symmetric, two-person coordination game, where Яц- = b_k for all k. This situation was first analyzed by Kandori and Rob (1995). Without loss of generality we can index the equilibria in decreasing order of welfare: fli > a₂ > • • • > a_K. The Pareto frontier consists of the payoff pair (Я], я,), and the assertion is that the stochastically stable outcomes are precisely those к such that = a\.

This result can be established quite simply as follows. Assume for simplicity that я_а > я* for all к > 2. Let us also assume that s/m is sufficiently small that the conventions are the only recurrent states of the unperturbed process. Represent each such state by a vertex

of a graph, and label the vertices 1.2................ K. By (9.5), the minimum

resistance edge exiting from vertex к > 1 is directed toward vertex 1, and its reduced resistance is strictly less than 1/2. On the other hand, every edge exiting from vertex 1 has reduced resistance at least 1/2. It follows that the tree rooted at vertex 1 and consisting of the

directed edges {(2.1), (3.1)............... (К, 1)} has a strictly smaller reduced

resistance than any other rooted tree. Hence it has minimum resis­tance among all rooted trees when the sample size s is sufficiently large. Thus equilibrium 1 corresponds to the unique stochastically stable convention.

9.7 The Kalai-Smorodinsky Solution

Suppose that the payoffs from the various contracts lie in a compact, convex set С с R². Suppose also that С is comprehensive: given any (a. b) 6 С, С contains all those pairs (a'. b') satisfying (0.0) < (ab') < (a. b). Assume finally that С contains a strictly positive payoff pair. Then С is a bargaining set, that is, a compact, convex, comprehensive, full-dimensional subset of R².

Given any such bargaining set C, let a⁺ = max {я : (я, b) e C) and b⁺ = max [b : (a. b) e C). The Kalai-Smorodinsky solution is the unique vector (я*, b') in С such that я*/я⁺ = b'/b⁺ is a maximum. Denote this maximum value by w⁺.

Discretize С as follows: for each small 8 > 0, let Cg consist of all pay­off vectors (a, b) e С such that a/8 and b/8 are strictly positive integers. Evidently, Сц -* С in the Hausdorff metric. Rescaling the utility func­tions if necessary, define w~(8) and w⁺(8) as in (9.2) and (9.3). Since С is comprehensive, w~{8) -* 0 as 8 -* 0. Since С is convex, w⁺(8) -*■ iv⁺ as5-+0. Defining a(«5) as in (9.4), it follows that ot(8) 0 as 8 -* 0. Hence the stochastically stable conventions guaranteed by theorem 9.1 must be close to the Kalai-Smorodinsky solution when <5 is small.

To formulate this result precisely, let us say that a pair (я, b) e Cj is stochastically stable if the associated convention is stochastically stable in pm.s.e f_{QT a}jj _suffi_ci_ent]y large s and all sufficiently small s/m.

Theorem 9.2. Let С be a bargaining set and let G_s be the pure coordination game with coordination equilibrium payoffs in C« for every small precision

S. As S becomes small, the stochastically stable payoffs converge to the Kalai- Smorodinsky solution of C.

9.8 Correlated Shocks

In this and preceding chapters, we have modeled stochastic variation by supposing that changes in behavior are driven by the accumulation of many uncoordinated, idiosyncratic choices. Of course, this is not the only way in which social change occurs. Sometimes individuals react to a common event, such as a technology shock. Or their expectations might be changed by the actions of a highly visible person (a role model). Without trying to downplay the variety and complexity of such stochas­tic influences, we can nevertheless say that they do not, by themselves, change the substance of the argument. To see why, consider a coordi­nation game in which the current norm is hj. To tip the process into the basin of attraction of some other norm h_k requires that at least fsr^l people demand regime к instead of regime j. When these changes arise from uncorrelated aberrations in behavior, each having probability e, the probability of this event is on the order of e^fsr'¹¹.

Now suppose instead that individuals do not change idiosyncrati- cally, but in groups. To be concrete, suppose that whenever an individ­ual makes an idiosyncratic choice, then for the next p — 1 periods it is certain that everyone in the same class will copy this choice. This cor­responds to the notion that new ideas affect everyone in a given class, but that after p periods, the idea wears off. (An example would be a book that extols the virtue of regime к over regime j.) Assume that the probability that a new idea will hit a given class in any given period is e. In this correlated version of the model, it takes only Isr^/p] "hits," each p periods apart, to tip the process from /), to h_k. When e is small, the probability of this event is on the order of еИ*/Р1. It follows that the stochastically stable norms in both the correlated and uncorrelated models minimize the same stochastic potential function (based on the reduced resistances r^) whenever s is sufficiently large relative to p.

While the framework described above is admittedly a stylized model of contract formation, it does contain some of the key elements that are surely relevant. These include the salience of precedent in shaping expectations, boundedly rational responses by individuals to complex environments, and idiosyncratic variation in behaviors. The precise way in which these features are modeled may alter the conclusions to some degree. Nevertheless it seems reasonable to conjecture that the most likely outcomes of such a process will tend to lie toward the "middle" of the feasible payoff set. The reason is that contractual relationships whose payoffs lie near the boundary tend to be unstable. They imply that some group is dissatisfied, and the more dissatisfied a group is, the more easily it is seduced by new ideas that give its members hope of getting more. Change, in other words, is driven by those who have the most to gain from change. Over the long run, this tends to favor contracts that are efficient and that offer each side fairly high payoffs within the set of payoffs that are possible.

Chapter 10

CONCLUSION

the theory we have sketched has two general implications. On the one hand, it demonstrates how high-rationality solution concepts in game theory can emerge in a world populated by low-rationality agents. Among the concepts we recover via this route are the Nash bargain­ing solution, the risk-dominant equilibrium in 2 x 2 games, iterated elimination of dominated strategies, minimal curb sets, and efficient equilibria in games of pure coordination. Moreover, in some types of extensive-form games, one obtains subgame perfect equilibrium and various forms of forward induction (Noldeke and Samuelson, 1993). Interpreted in this way, the evolutionary approach is a means of recon­structing game theory with minimal requirements about knowledge and rationality.

Interpreted more broadly, the theory suggests how complex economic and social structure can emerge from the simple, uncoordinated actions of many individuals. When an interaction occurs over and over again and involves a changing cast of characters, a feedback loop is established whereby past experiences of some agents shape the current expectations of other agents. This process yields predictable patterns of equilibrium and disequilibrium behavior that can be construed as social and eco­nomic "institutions," that is, established customs, usages, norms, and forms disorganization. Although we have taken games as our basic model of interaction, the theory can be applied to many other forms of interaction, as we illustrated with the neighborhood segregation model.

Admittedly, there is a considerable gap between the simple models of interaction that we have studied and the economic and social institu­tions that we see around us. One would be hard-pressed, for example, to identify the complete set of rules and incentives that govern the nego­tiation and enforcement of economic contracts. It would be even more difficult to write down the game that represents, say, interactions in the workplace or the family. Nevertheless, these institutions can be thought of as equilibria in appropriately defined, high-dimensional games. The same goes for conventions of correct or morally acceptable behavior. We sometimes refer to these as "norms" instead of "conventions," thus expressing the idea that deviations from the norm may be punished. For our purposes, however, this is not a fundamental distinction: norms can also be represented as equilibria in a repeated game, where social op­probrium and other forms of punishment are the expected responses to deviations from the norm (and those who fail to carry out the appropri­ate punishments may themselves be punished). Our theory applies to all of these situations: people develop expectations about how others behave through repeated interactions and experience of others' interac­tions, which eventually coalesce into recognizable patterns of behavior.

Even if we grant, however, that customs and norms can be thought of as equilibria in games, is it true that they arise through the accretion of many uncoordinated decisions, or do they arise through the concerted and deliberate action of a few key people? Obviously it would be absurd to claim that they arise only in the former manner. Many institutions and patterns of behavior have been shaped, at one time or another, by influential people who endorsed (or enforced) a particular way of do­ing things. Napoleon instituted the legal code that still governs much of continental Europe; Bismarck established a social security system for industrial workers in Germany that served as a model for many later systems;¹ Catherine de Medici made it fashionable in France to use a fork at dinner.² Major players obviously matter in the development of economic and social institutions, but this does not imply that minor players do not matter. Actions by major players stand out and are easy to identify; small variations in individual behavior are more subtle and difficult to pinpoint, but may ultimately be more important for the de­velopment of some kinds of institutions. Moreover, we suspect that influential actors often get credit for things that were about to happen anyway.

Even if major players do sometimes matter, they may be minor rela­tive to the scale of the social institution under consideration. Consider the evolution of language: Is it governed by major or minor players? Words become current in part through street talk, in part through ed­ucation, and in part through dissemination by the media. It is hard to say which matters more over the long run. It should also be remem­bered that coordinated decisions by large groups of players are often quite small in the overall scheme of things. Consider the teaching of a second language, such as Chinese or Japanese, in the United States. The choice of which languages to offer are usually made by schools rather than by individuals, so we might think that the choice is gov­erned by "large" players. The fact is, however, that there are many schools, and they often make choices in an uncoordinated way. Schools in Nebraska probably do not coordinate their language curricula with schools in Iowa. Even if they did, they would almost certainly not co­ordinate their choice with schools in Germany. At almost any level we can conceive of, these decisions are made in a fairly decentralized way relative to the whole. Moreover, it is the whole that matters: the value of learning a second language depends on the number of other people in the world who learn it. The players in this coordination game can be very large indeed (countries) and still be quite small on the scale of the whole process.

A similar argument can be made for the evolution of many other types of institutions: the adoption of currencies, the use of particular kinds of contracts (e.g., rental contracts, employment contracts, marriage con­tracts), codes of socially acceptable behavior, acceptable punishments for deviations from socially acceptable behavior, and so forth. All such forms of interaction are sustained as institutions through the mutually consistent expectations of society's members. Change is driven in part by small individual variations that tip expectations into a new equi­librium, and in part by the concerted actions of influential individuals and groups. We have emphasized the role played by the small players, while not denying the importance of the larger ones.

Another important issue is the rate at which change occurs. Change is driven in part by the underlying dynamics of adjustment and in part by idiosyncratic shocks. The former will typically operate more quickly than the latter. In practice, this means that the trajectory of the process in the short run will be strongly influenced by initial conditions, and the dynamics will be fairly well approximated by the expected motion. Idiosyncratic shocks will be felt only over the longer run, as various regimes become established and are later undone. The length of time needed for these regime transitions depends on the size of the stochastic shocks and the degree of correlation between them, the amount of in­formation agents use in making their decisions, and the extent to which they interact in small, close-knit groups. It should also be recalled that the waiting time in these models is measured in "event" time, and thou­sands or even millions of distinct events maybe compressed into a short interval of "real" time. Thus the length of the long run depends cru­cially on the details of the learning environment. In general, however, it should come as no surprise to find societies that operate for long periods of time in regimes that do not correspond with the long-run predictions of the theory. Institutions, once established, can lock people into estab­lished ways of thinking that are hard to undo. Nevertheless established institutions can be undone, and over time they are.

The preceding chapters have outlined a general approach to study­ing the dynamics of institutional change, based on a simple model of decentralized agents who adapt their expectations and responses to a changing environment. We assumed in particular that people form simple statistical models to predict how others will behave in a given situation. Usually (but not always) they choose myopic best replies given their expectations. Obviously many variants and elaborations of such a learning process can be imagined, some of which were discussed in Chapter 2. It is natural to ask, for example, how sensitive the results are to different ways of specifying the learning rule. It would be par­ticularly interesting to examine the behavior of a population composed of different types of learners: some who employ statistical forecasts, others who imitate, and still others who respond in Pavlovian fashion to payoffs from past experience.

Another elaboration of the model would recognize that interactions between players are to some extent endogenous.³ The probability that two players will meet may depend on the history of the process to date— on the number of times they met before, on the payoffs that resulted from their previous interactions, and so forth. In a model where individuals trade goods, for example, large gains from trade might well reinforce the probability that agents will trade in the future. This would lead to the endogenous formation of trading networks. In situations where people interact socially, one could imagine that there would be a ten­dency for people to select partners who are like themselves along such dimensions as ethnicity, income, language, and geographical location. One could further suppose that the fact of interacting makes them even more similar. Such a process can congeal into distinct tribes or castes that have many internal interactions but only limited contact with each other.⁴ In the presence of repeated shocks, one should be able to predict the relative likelihood that stratified (or integrated) configurations will emerge over the long run. The point of this study has been to sketch a general framework for tackling these questions, rather than to argue that any single learning rule is correct, or that any one model of social interaction is more realistic than another.

There are, nevertheless, several qualitative features of such processes that are likely to be robust under different model specifications and that are subject (at least in principle) to empirical verification. To illustrate these features concretely, imagine a population divided into many sim­ilar subpopulations, or "villages," that do not interact with one another. (They might be located on different islands, for example.) Consider a form of interaction—a game—that is played recurrently in each of the villages, and suppose that this game has multiple strict Nash equilibria. For example, the interaction might involve a principal and an agent who are trying to coordinate on the form of the contract that will govern their relationship. Suppose further that the system is subjected to persistent idiosyncratic shocks that are small but not vanishingly small. The fol­lowing three features are valid for the adaptive dynamics analyzed here, and no doubt hold for a considerably wider class of stochastic learning processes.

Local conformity, global diversity. Within each village, at any given time, behaviors are likely to be close to some equilibrium (the local convention), though idiosyncratic, unconventional behaviors will be present to some degree. Different villages may operate with different conventions due to historical chance.

Punctuated equilibrium. Within each village, there will tend to be long periods of stasis in which a given equilibrium remains in place, punctu­ated by occasional episodes in which the village tips from one equilib­rium to another in response to stochastic shocks. Thus there is temporal diversity in a given place as well as spatial diversity at a given time.

Equilibrium stability. Some equilibria are inherently more stable than others, and, once established, they tend to persist for longer periods of time. The relative stability of different equilibria will tend to be reflected in the frequency with which they occur among the various villages at a given point in time (and also within each village over a long period of time). When the stochastic perturbations are small, the mode of this frequency distribution will be close to the stochastically stable equilibrium with high probability.

The challenge to theory is to determine whether these and related qualitative predictions are borne out by empirical evidence. In looking for evidence, one would want to focus on games that are played fre­quently by changing partners, in which precedent plays an important role in shaping expectations, and in which there are positive reinforce­ment effects from conformity (as in a coordination game). Forms of con­tracts are natural candidates because their enforcement is carried out by courts, which tend to rely on precedent to determine the meaning of contract terms and the remedies for default. Standards of professional practice (in medicine, accounting, or law) may lend themselves to a sim­ilar type of analysis. Means of communication, including the evolution of language, also have many of the relevant characteristics. The reader will no doubt think of other examples.

Of course, the theory developed here, like all theories, abstracts away from complications that inevitably arise in applications. One compli­cation is that games change over time. If they change too rapidly, the adaptive learning process may not have time to settle into its long-run pattern. In these situations the transient rather than the asymptotic behavior of the adaptive process should occupy center stage in the anal­ysis. A second complication is that games, and the conventions they generate, cannot always be treated in isolation. Almost every game we can think of is embedded within a larger game. Bargaining over con­tract forms takes place within the shadow of the law, the law operates within the penumbra of morality, morality is colored by religious belief. Norms and customs from one sphere inevitably spill over into differ­ent spheres; there are no clear boundaries delimiting our relations with others. Doubtless all of these interactions could be written down as one large game. Equally doubtless they never will be.

Still, we must begin somewhere. Just as perfect spheres and friction- less planes are idealized but useful concepts for modelling mechanical interactions, so we can view games and learning rules as primitives for modelling social and economic interactions. While our approach cannot be expected to predict the history of any single institutional form, it does suggest that institutions evolve according to specific spatial and tempo­ral patterns, and that there is a relationship between the durability of institutions and their welfare implications for individuals.

Date: 2016-04-22; view: 511