
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Figure 3.2. Alternative paths to different absorbing states.likelihood that the process will be in each state z at each future date t independently of the initial state, as long as t is large. In most cases, solving for the stationary distribution by algebraic methods is impracticable because of the large number of states. In the next section we show how to get a handle on the stationary distribution by a different technique. 3.4 Perturbed Markov Processes Consider a Markov process P° defined on a finite state space Z. A perturbation of P° is a Markov process whose transition probabilities are slightly perturbed or distorted versions of the transition probabilities P^z,. Specifically, for each e in some interval [0, £*] let P' be a Markov process on Z. We say that Pe is a regular perturbed Markov process if Pr is irreducible for every e e (0. £*], and for every z, z' e Z, P'l:. approaches P^z. at an exponential rate, that is, limP^. = P^, (3.11) «-♦o and if Pt2. > 0 for some e > 0, then 0 < lim PL,/sr(z-z,) < oo for some r(z, z') > 0. (3.12) The real number r(z. z') is called the resistance of the transition z -> z'. Note that r(z, z') is uniquely defined, because there cannot be two distinct exponents that satisfy the condition in (3.12). Note also that P^, > 0 if and only if r(z, z') = 0. In other words, transitions that can occur under P° have zero resistance. For convenience, we shall adopt the convention that r(z, z') = oo if P^, = P^z, = 0 for all e e [0. £*], so that r(z, z') is defined for all ordered pairs (z, z'). Since P is irreducible for each e > 0, it has a unique stationary distribution, which we shall denote by pr. A state z is stochastically stable (Young, 1993a) if lim pe(z) > 0. (3.13) As we shall show in theorem 3.1 below, limf_oME(z) = p°(z) exists for every z, and the limiting distribution is a stationary distribution of P°. It follows in particular that every regular perturbed Markov process has at least one stochastically stable state. Intuitively, these are the states that are most likely to be observed over the long run when the random perturbations are small. In a moment we shall show how to compute the stochastically stable states using a suitably defined potential function. First, however, let us observe that adaptive play with parameters m, s, e is a regular perturbed Markov process. Given an //-person game G with finite strategy space X = Ï X„ the process operates on the finite space X'" of length-/// histories. Given a history /j = (.ã1, x2,.... xra) at time t, the process moves in the next period to a state of form //' = (x2, x3......... xm, x) for some x e X. Any such state //' is said to be a successor of //. Before choosing an action, an /'-player draws a sample of size s from the /// previous choices in h of each class j Ô i, the samples being independent among distinct classes j. The action x, is an idiosyncratic choice or error if and only if there exists no set of // — 1 samples in h (one from each c'lass j Ô /') such that x, is a best reply to the product of the sample frequency distributions. Note that the concept of error depends on the preceding state //. For each successor //' of h, let r(h, W) denote the total number of errors in the rightmost element of//'. Evidently 0 < r(/z. //') < //. It is easy to see that the probability of the transition // —► //' is on the order of £n', ', )(l — e)n~r(h h ), where we omit a multiplicative constant that is independent of e. If //' is not a successor of //, the probability of the transition h -» //' is zero. Thus the process pm.s.f approaches Pm s0 at a rate that is approximately exponential in e; moreover it is irreducible whenever e > 0. It follows that Pmsc is a regular perturbed Markov process. We will now show how to compute the stochastically stable states for any regular perturbed Markov process P' on a finite state space Z. Let P° have recurrent classes £i, £2........... EK. For each pair of distinct recurrent classes E, and £,, i ô j, an ij-path is a sequence of states f = (zi, z2................ z,() that begins in E, and ends in E;. The resistance of this path is the sum of the resistances of its edges, that is, r(0 = ã(ãú z2) + r(z2, z3) + - • - + r(z,_ü z,). Let r,y = min r(£) be the least resistance over all //-paths f. Note that by the definition of a recurrent class, Ã/, must be positive, because there is no path of zero resistance from E, to £,. Now construct a complete directed graph with Ê vertices, one for each recurrent class. The vertex corresponding to class £; will be called j. The weight on the directed edge /' j is r,y. Figure 3.3 shows an illustrative example with three classes. A tree rooted at vertex j (a j-tree) is a set of Ê — 1 directed edges such that, from every vertex different from j,
there is a unique directed path in the tree to The example shown in Figure 3.3 has three /'-trees rooted at each vertex j, and nine rooted trees altogether (see Figure 3.4). The resistance of a rooted tree T is the sum of the resistances r,y on the Ê -1 edges that compose it. The stochastic potential y, of the recurrent set £, is defined as the minimum resistance over all trees rooted at j. Intuitively, when the noise parameter e is small and positive, the process is most likely to follow paths that lead toward the recurrent classes having minimum potential. This suggests that the stochastically stable states are precisely those that sit in the classes having minimum potential. Formally this result can be stated as follows.5 THEOREM 3.1 (Young, 1993a). Let P' be a regular perturbed Markov process, and let ö' be the unique stationary distribution of Pf for each e > 0. Then limF^opR = p° exists, and p° is a stationary distribution ofP°. The stochastically stable states are precisely those states that are contained in the recurrent class(es) ofP41 having minimum stochastic potential. We illustrate this result for the typewriter game with learning parameters m = 4 and s = 2. We have already seen that the unperturbed process (with e = 0) has exactly two recurrent classes, each consisting of
a single absorbing state: Ei = |all-D| and E2 = (all-Q). We need to find the least resistant path from E\ to E2, and also from E2 to E\. Consider the first case. If the process is in the all-D state, and exactly one player makes an error (plays Q), then we obtain a state such as the following: DDDQ DDDD In the next period, both players will choose D as a best reply to any sample of size two; hence, if there are no further errors, the process will revert back (after four periods) to the state, all-D.
Suppose now that two players simultaneously make an error, so that we obtain a state of the following form:
there is a unique directed path in the tree to /'. The example shown in Figure 3.3 has three /'-trees rooted at each vertex /', and nine rooted trees altogether (see Figure 3.4). The resistance of a rooted tree à is the sum of the resistances r,; on the Ê -1 edges that compose it. The stochastic potential ó\ of the recurrent set Ej is defined as the minimum resistance over all trees rooted at j. Intuitively, when the noise parameter e is small and positive, the process is most likely to follow paths that lead toward the recurrent classes having minimum potential. This suggests that the stochastically stable states are precisely those that sit in the classes having minimum potential. Formally this result can be stated as follows.5 Theorem 3.1 (Young, 1993a). Let Pf be a regular perturbed Markov process, and let ö' be the unique stationary distribution of P' for each e > 0. Then Èòå->îð,å = exists, and pP is a stationary distribution ofP°. The stochastically stable states are precisely those states that are contained in the recurrent class(es) of P° having minimum stochastic potential. We illustrate this result for the typewriter game with learning parameters m = 4 and s = 2. We have already seen that the unperturbed process (with e = 0) has exactly two recurrent classes, each consisting of E, I----- 4----- *E,
Date: 2016-04-22; view: 578
|
 Figure 3.3. A complete directed graph on three vertices with resistances on edges.
Figure 3.3. A complete directed graph on three vertices with resistances on edges.



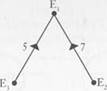


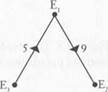
 Figure 3.3. A complete directed graph on three vertices with resistances on edges.
Figure 3.3. A complete directed graph on three vertices with resistances on edges.

 Figure 3.4. The nine
Figure 3.4. The nine