
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
V. PRACTICAL OPTIMIZATION
http://education-portal.com/academy/lesson/optimization-and-differentiation.html#lesson
Numerical Search
Numerical search procedures underlie numerical optimization methods. There is voluminous material to discuss in this field (Gill, et al., 1981); we overview the topic by considering the basic technique of gradient search, and by touching briefly on the technique of sequential quadratic programming.
Steepest Descent
http://www.youtube.com/watch?v=1lL6WXlc9NE
Given no other information about a function other than its continuity and its expressive form f:RnŪR, how can one find points 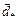 where f is minimum? We need to determine where the f's derivative is zero, but we do not have an expression of its derivative.
where f is minimum? We need to determine where the f's derivative is zero, but we do not have an expression of its derivative.
In a design space of one dimension R one method for finding the minimum of a function is sub-division search. In such methods, a function : f:RnŪR, is minimized over an initial "wide" interval [a,b]ÌR The interval [a,b]is iteratively subdivided, the function is evaluated at a point in each subdivision, and the half with a higher returned value is eliminated from further exploration (divide and conquer). Functions that are bounded and do not have many local minima within [a,b]work well for this solution strategy; more complex functions present numerical difficulties.
In a design space of n dimensions, the search is more complicated than sub-division search due to the multiple dimensions. We can search along many different unit vectors. An effective method is to sub-division search along the direction of the function that is decreasing most quickly, or over the one-dimensional line along the gradient Ñf There are many forms of such gradient search methods (Gill et al, 1981), such as conjugate gradient methods, that ensure the search path remains focused on the overall steepest path.
Linear Programming
http://www.youtube.com/watch?v=dbcK3fE0tzU
Constrained optimization presents further difficulties than simply searching anywhere in Rn. Consider a simplified subset of all possible constrained optimization problems, the set of problems when all of the constraints are linear equations. In this case, one must determine the solution point that minimizes f subject to linear h and g constraints.
In this situation, different solution methods are available than steepest descent methods. One can think of linear equations as hyper-planes in Rn. If f is linear, or quadratic, then it is monotonic. In this special case, the minimum of f must occur at a constraint boundary. Constraint boundary extrema occur where the constraint hyperplanes intersect. This means that one can reduce the search from all of Rn to those points where the constraint boundaries intersect. Conceptually, one can list the finite number of hyperplane intersection points and minimize f only over these few points. This form of search, called simplex search, can be carried out very rapidly (Gill, et al., 1981), with relatively reduced computational effort.
Date: 2016-01-14; view: 970
| <== previous page | | | next page ==> |
| Equality Constraints | | | Sequential Quadratic Programming |