Solution Definition

Consider a full engineering model of a product. As a first step, we may want to consider typical values for every noise variable (Chapter 19 considers the full impact of noise). This approach simplifies the noise space to a single point. Each noise variable is then called a "constant" of the formal design problem. (Note: From now on, every time we hear the word "constant" in an analysis technique, it should set off a warning bell. Physically, how constant is it? What is the constant's range of variation? How is it set? How is it measured?) We may then consider one of the performance metrics, and determine the configuration in the design space that maximizes the performance. Typically, classical optimization methods represent performance metrics that seek the smallest values, i.e., minima. Given this description, a performance metric

can be minimized by finding d* such that

This result is the minimum solution (f(d*) = min(f(d))) to the analytically posed and formulated design problem. Similarly for performance metrics that have a target value, we can define a minimization by the variation from a target

This approach demonstrates the problem formulation for all optimization problems. Basically, we set up a search. This formulation has two aspects:

• What do we search for? What is "best" in a formal way? Here, it is the minimum of the product performance metric.
• What do we search across? What bounds D? What is feasible, and what do we know is available?

These are, at the core, problem definition issues. They are not computational complexity problems or numerical problems. What do we want to achieve from the product?

Pareto Optimality

https://www.youtube.com/watch?v=ictUYjkQeZU

One answer to the previous question is to improve all of the performance criteria, subject only to basic availability constraints. We might then try to minimize the cost and also maximize the performance criteria. This approach is not always possible. For example, when booking a flight, we cannot acquire a ticket that provides the best service at minimum cost. Two objectives exist in this case: greatest comfort (first class) and, at the same time, lowest cost (coach seating). We can either buy a ticket that makes us most comfortable-the first class ticket solution that compromises the cost objective, or we can buy a ticket that is inexpensive-the coach ticket solution that compromises the inflight service objective.

We might think about this situation in terms of the model spaces and P (Chapter 13). The constraints define a feasible sub-region S of D that are available and, consequently, are possible, as shown in Figure 16.3. We might think of the mappings fi together as a vector mapping

and work to minimize this vector p. Consider mapping every point in S through Equation (16.5), thereby defining a feasible space Z in P. This result is shown in Figure 16.4.

In the performance space, we know that we want to minimize the performance metrics P_j. Yet notice an interesting feature of Figure 16.4

.

The space Z is not shaped so that P₂ and P₂ can be simultaneously minimized. The point P₁< minimizes P₂ in the feasible space, and point P₂<minimizes P₂ in the feasible space. All points along the short boundary of Z, connecting and P₁< and P₂<' minimize some weighted combination of P₁< and P₂<' In other words, there are many optimal solutions, each which optimizes a different weighted combination of the criteria.

Put this in the example context of booking an airline flight. All flights that reach the destinations are the space of feasible alternatives. We might consider the variable P₁ to be price, and the variable P₂ to be flight time. Across all airlines and their provided routes, the one airline ticket that provides the shortest flight time (has a direct flight, for example) is the point P₁<' The airline ticket that has least price is the point P₂<' probably by an airline that requires a layover in a hub airport and uses a small propeller plane for part of the journey. Further, there are tickets that perhaps are not least cost nor shortest flights, but are an optimal compromise between these two concerns such as a moderately priced flight with a layover using all jet service. Consider, though, a point Pa as shown in Figure 16.4. It has the same level of performance on P₁ but worse performance on P₂' Under these circumstances, it would not be rationally selected as a solution. One could always instead choose P₂< instead. For example, if two airlines offer flights at the same cost (P₁)' the flight that has fewer layovers and so a shorter flight time (P₂) is a better solution. Similarly, if two concepts provide the same performance (P₁)' the one that uses less costly components (P₂) is a better solution.

This basic thinking is the principle behind what is known as Pareto optimality. A point P is Pareto optimal if the only way to improve any of its components Pi is by worsening other components Pj' All such points basically lie in the lower quadrant boundary of the space Z, as shown in Figure 16.5. This region is also called the Pareto Frontier, denoted by F. Any point in F can be a reasonable optimal solution.

This idea has implications when determining a solution to a modeled design problem. One must search across the design variable space for a useful solution as above. Once found, however, one should then explore around this point by changing the variables, and obtain a feel for how much improvement one can attain in some of the performance variables at how much sacrifice of the others. A different point on the Pareto frontier may offer better overall performance.

Pareto optimality provides a sensible approach for making decisions in the midst of conflicting objectives. However, this concept does not obviate the responsibility of a designer to seek solutions to design problems that remove conflicts altogether. If conflicts may be removed through a drastic change or metamorphosis of a design configuration, a compromise will not be needed, potentially improving all performance variables. While conflicts will exist in all practical product development, removing as many conflicts as possible will result, by necessity, in novel product solutions. Novel solutions should be our primary mission. Therefore any design problem solution, model optimal or otherwise, is permitted as final only after resources have been expended.

A design team should accept an optimal solution only when they are to the point where they cannot go back to develop new concepts that remove trade-offs (Chapter 10).

https://www.youtube.com/watch?v=gpcmnR7CtZM

III. BASIC METHOD: SPREADSHEET SEARCH

A basic method to explore and solve product models is what we call a spreadsheet search.

There are no data types such as integers, vectors, matrices, etc., instead every number is a floating point number. Further, algorithms with loops are difficult to implement. In terms of product design, we wish to solve a model to determine preferred design variable values and gain insight into the physics and sensitivity of how a product will perform. This concept of what an ideal design model would be is shown in Figure 16.6 (after Serrano). In this figure, design variables are input through designer queries. Adjustments are inputs to a product model representing product responses to the end users' queries. Noise variations from sources such as manufacturing, material, and wearout may also be explored. When limits or constraints are violated with the query, a signal is produced notifying the designer or end user.

Spreadsheets can satisfy these model solution goals, at least at a basic level, through a series of steps executed by the designer. These steps may be classified, broadly, into two categories: (1) planning and design of a product model worksheet, and (2) developing and executing a solution procedure. Let's consider these categories for a product model worksheet. The first category involves the implementation of four basic steps. The first step is to identify the purpose of the worksheet. This step entails the title of the worksheet, writing a one-line concise statement of its purpose. Information for this step comes directly from the product model we are attempting to solve.

The next step is to determine the outputs that are desired from worksheet analysis. The outputs, for product development, are the metric values that represent the customer needs. Again these are determined from the product modeling results. However, it is important to also identify intermediate results that should be displayed as outputs. Intermediate results are necessary to validate a model (i.e., compare it to known or simple solutions) and to obtain particular physical insights that may be used to improve a product.

Once the outputs are chosen, the inputs should be identified. The inputs are of two forms, from the product model: noise variables and design variables. Noise variables may be initially viewed as "constants" and then later varied during model analysis to understand their impact on performance. (Chapter 19 studies more complete methods for handling noise variables as part of robust design.)

Design variables, on the other hand, represent the decisions we are seeking to make as part of the model solutions. These variables should be clearly displayed in the worksheet, in addition to their boundaries or ranges of choice. This information, again, may be extracted from the product model.

Product Application: Spreadsheet Search for a Toy Rocket Product

http://www.youtube.com/watch?v=XEB9CHSLNus

To illustrate the use of a spreadsheet for solving product models, let's consider the design of a toy rocket. As illustrated in Figure 16.7, this product uses water and compressed air to launch a lightweight, singlestage rocket. The first introduction of this product occurred during the mid-1950's by Park Plastics Company, based on a German Patent (Dixon).

Single-stage compressed-air-water rockets are still popular toys today. We wish to design a portfolio of plastic rockets that will satisfy a number of customer needs, ranging from power and high flight to safe operation and inexpensive production. For the purposes of this example, let's focus on the performance of the rocket, i.e., high-vertical flight. The basic operation of the rocket is to fill the hollow fuselage of the rocket with water, using a fill cup. Only a percentage of the total rocket is used to allow the remaining air volume to be pressurized. After filling the rocket with water, a hand pump is attached to the rocket, and the rocket is rotated to a vertical-up position for firing. The lock forms a seal between the rocket and the pump. It also provides a release mechanism for the rocket off of the launching pad (i.e., the pumpfunction sharing).

After the rocket is rotated to a vertical position, the hand pump is used to pressurize the rocket (using 20-30 strokes). The design is based on the ability of a young child to pump a large bicycle tire; thus, 20-30 strokes result in 50 to 65 psi (340 to 440 kPa) gauge pressure.

The rocket is then released. The air acts as a piston to push the water out the nozzle of the rocket. The momentum transfer from the water leaving the rocket accelerates the fuselage vertically (assuming that the rocket is aimed up). After the water exits the nozzle, only gravity and drag forces are acting on the rocket, implying that it will reach a final height, depending on its initial velocity from the transfer of water momentum, at the instant the water exits or when the pressure in the rocket reaches atmospheric pressure.

Based on this description, and based on the customer need of soaring as high as possible, an engineering model is developed for the rocket travel. This model assumes that the rocket can range across a number of sizes (initially a 5.5 in. [14.0 cm] height and 1 in. [2.54 cm] diameter fuselage due to molding constraints). It also utilizes the momentum equation from fluid mechanics, continuity (conservation of mass), isentropic thermodynamic process of initially pressurizing and subsequent expansion of the air, and Bernoulli's equation (assuming incompressible and steady-flow of the water flux through the nozzle).

Based on these assumptions, the model may be described by a set of simultaneous equations, applied in the accelerating reference frame (control volume) of the rocket. These equations will predict the height of the rocket as a function of the design variables (such as rocket volume, rocket shape, nozzle diameter, etc.). This model is represented as

where m is the total rocket mass (with water) as a function of time, V_r is the rocket velocity, g is the gravitational constant, C_d is the drag coefficient, P_a is the density of air, A_r is the cross-sectional area of the fuselage, P_w is the density of water, V_n is the jet velocity across the nozzle as a function of time, A_n is the area of the jet (nozzle), mw is the mass of the water (as a function of time), C_n is the nozzle coefficient, P_a is the pressure of the air (as a function of time), Patm is the ambient pressure, C is the isentropic constant for the air expansion, V_r is the volume of the rocket, and k is the ratio of specific heats. The model given by Equation (16.6) is valid to the time where the water is ejected from the rocket. After this point, the momentum equation simplifies to

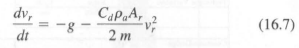
where m is the mass of the rocket fuselage (constant).

Based on the product model in Equations (16.6-7), we may apply the spreadsheet method to design a worksheet to solve this model. First, the purpose of the spreadsheet is to calculate rocket heights for varying operating conditions (initial pressure and percent volume of water) and for the choices of design variables (rocket volume, etc.). The purpose is also to investigate the validity of the rocket concept and its extremes, such as determining the time required for the water to eject from the rocket (inertial effects). In conjunction with this worksheet purpose, the inputs to the model are the variables described by Equations (16.6-7), except for the velocity of the rocket and jet. These two remaining variables are the output and an intermediate variable, respectively.

The output of the model is velocity of the rocket as a function of time, integrated to calculate the vertical height. With the inputs and outputs defined (as bounded by plastics' manufacturing and ergonomics), a strategy must be developed for solving the model and creating a worksheet layout. Assuming a relatively wellbehaved system, Equation (16.6) is converted to a discrete form using Euler's method. Based on this form, a small time step is chosen and checked for convergence, and the equations are solved iteratively until the mass of the water is zero or until the pressure in the water reaches atmospheric conditions. To solve the equations iteratively, initial values of rocket velocity, water mass, air pressure, and jet velocity are given. A new jet velocity is calculated at the instant the rocket is released, followed by a new rocket velocity. The exiting water mass and expanding air pressure are updated for these new values, and the cycle repeats.

Figure 16.8 shows a spreadsheet layout that corresponds to this strategy. The worksheet shown in Figure 16.8 arranges the inputs, initial conditions, and calculations in a blocked format. The resulting outputs, given the iterations shown at the bottom of the worksheet, are the velocity of the rocket, initial height, and remaining water in the rocket after the acceleration stage of travel. Notice in the worksheet that only the operating conditions are under examination at this point. That is, it is important to understand the preferred values of percent volume of water and initial air pressure before studying the ranges of design variable choices. The worksheet need only vary the design variable values to study their effects.

A second worksheet is created to calculate the final height of the rocket based on Equation (16.7). This worksheet, shown in Figure 16.9, references the outputs of the first worksheet and iteratively solves for the rocket height, defined by when the velocity of the rocket becomes zero.

This height value is shown in the output block of the worksheet. A third worksheet is also created to aggregate the results of the simulations for ranges of operating conditions. Figure 16.10 shows the

summary worksheet, in addition to an output plot of the rocket height versus the operating variables.

For the sake of calibration and validation, the original Park Plastics' rocket may be experimentally tested, recording rocket heights as a function of initial air pressure and water volume. To provide a valid comparison, the simulation in the first three worksheets must be run based on the Park Plastics' geometry. Figure 16.11 schematically presents the experimental setup for the tests. Notice that a two-point sight system with triangularization is used to measure the rocket height. The angle measured with respect to the horizon is recorded, in addition to the horizontal distance from the sight system to the point where the rocket reaches its apex.

Given this experimental setup, tests on the Parks Plastics' rocket are conducted by first mounting a pressure gage in line with the pump (to measure initial air pressure). The hand pump shown in Figure 16.7 is modified for this purpose. A launch rod is also fabricated to guide the release of the rocket.

Water is then introduced into the rocket with a syringe; the rocket is pressurized, attached to the launch pole, and released. Measurements are taken by two sighting systems at varying distances from the launch location, and all data are recorded. The height for each test run is calculated based on the sighting angle, initial sight height, and distance from the launch location.

Implementing this test procedure, test data are shown in Figure 16.12. In addition, the simulation data are plotted on the same axes. Notice from the figure that some variation occurs between the model results and the test data. However, the overall results are very consistent in trends and magnitudes!

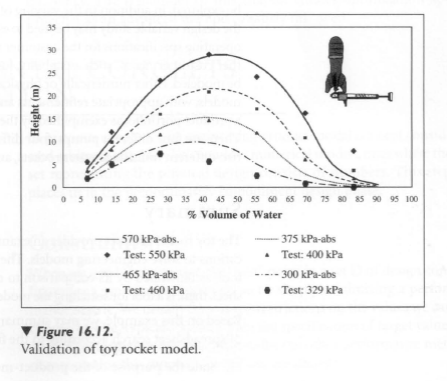
The model appears to need very little adjustment in physical constants or other model variables. The limits of the model must now be explored, in addition to the varying of design variables. The results of the design variable study may be used to establish the rocket geometry and operating specifications for the customer needs under consideration. Further customer needs, such as stability, low cost, durability, etc. may also be modeled, either numerically or physically. Design decisions from these models, with appropriate refinements and prototype testing, can lead to a product portfolio, as exemplified by the rockets shown in Figure 16.l3. There are four different pumps, four different single stage water rockets, two different multistage water rockets, and one 2-liter bottle rocket kit.

Summary

The toy rocket product provides an example of using spreadsheet applications to solve engineering models. The model is a powerful predictive tool, as illustrated by its comparison to experimental results. A spreadsheet, then, is a tool for searching the model to determine design solutions. Based on this example, we may summarize the basic numerical model of spreadsheet search according to the following steps:

1. State the purpose of the product-model worksheet(s).

2. Identify the outputs desired from the worksheet.

3. Identify the inputs, constants and design variables.

4. Determine the calculations needed to map inputs to outputs.

5. Create a layout for the worksheet that adds utility in solving for design choices.

6. Develop a strategy for solving the calculations within the worksheet(s).

7. Explore the Pareto frontier and vary the constants (potential noise parameters) .

This method, as embodied by seven high-level steps, is very effective for solving product models.

Date: 2016-01-14; view: 765