Interstitial void spaces

The atoms in each layer in these close-packing stacks sit in a depression in the layer below it. As we explained above, these void spaces are not completely filled. (It is geometrically impossible for more than two identical spheres to be in contact at a single point.) We will see later that theseinterstitial void spaces can sometimes accommodate additional (but generally smaller) atoms or ions.

If we look down on top of two layers of close-packed spheres, we can pick out two classes of void spaces which we calltetrahedral and octahedral holes.

Tetrahedral holes

If we direct our attention to a region in the above diagram where a single atom is in contact with the three atoms in the layers directly below it, the void space is known as atetrahedral hole. A similar space will be be found between this single atom and the three atoms (not shown) that would lie on top of it in an extended lattice. Any interstitial atom that might occupy this site will interact with the four atoms surrounding it, so this is also called a four-coordinate interstitial space.

Don't be misled by this name; the boundaries of the void space are spherical sections, not tetrahedra. The tetrahedron is just an imaginary construction whose four corners point to the centers of the four atoms that are in contact.

Octahedral holes

Similarly, when two sets of three trigonally-oriented spheres are in close-packed contact, they will be oriented 60° apart and the centers of the spheres will define the six corners of an imaginary octahedron centered in the void space between the two layers, so we call these octahedral holes or six-coordinate interstitial sites. Octahedral sites are larger than tetrahedral sites.

An octahedron has six corners and eight sides. We usually draw octahedra as a double square pyramid standing on one corner (left), but in order to visualize the octahedral shape in a close-packed lattice, it is better to think of the octahedron as lying on one of its faces (right).

Each sphere in a close-packed lattice is associated with one octahedral site, whereas there are only half as many tetrahedral sites. This can be seen in this diagram that shows the central atom in the B layer in alignment with the hollows in the C and A layers above and below.

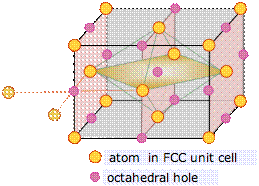The face-centered cubic unit cell contains a single octahedral hole within itself, but octahedral holes shared with adjacent cells exist at the centers of each edge.

Each of these twelve edge-located sites is shared with four adjacent cells, and thus contributes (12 × ¼) = 3 atoms to the cell. Added to the single hole contained in the middle of the cell, this makes a total of 4 octahedral sites per unit cell. This is the same as the number we calculated above for the number of atoms in the cell.

Date: 2016-01-03; view: 2702