
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Harmonic oscillations of physical pendulum
Harmonic oscillations are the type of free oscillations, which the system performs under activity only of restoring force. The restoring force is a force acted to the centre of gravity of a system and always directed to equilibrium position. The restoring force as well is termed as quasi-elastic force, because for its describing introduce the elasticity equation: FREST = kqe×x, (9) where x displacement from equilibrium position; kqe quasi-elastic coefficient. Negative sign on the right hand side of the equation (9) means that the restoring force always acts in the opposite direction of the displacement. The role of restoring force is fulfilled usually by the total of gravity force and supporting or spring force. Natural system is an ideal physical model of system with no any energy losses. In the real-world systems there are always act different kind of damping forces, which increase period and decrease amplitude of oscillations (see Laboratory work Ή 4-3). Regime of oscillations without of losing energy is termed eigenmodes and frequency of such oscillations eigenfrequency. Parameters of eigenmodes of oscillations are being identified by 0 index. Lets consider natural mechanical oscillations of physical pendulum (Fig.1). Physical pendulum is a rigid body suspended from a fixed point in it, free to pivot about some horizontal axis through that point under the force of gravity. The oscillations description method is in building and solving of differential equations for appropriate motions. If the pendulum shifted from its equilibrium position then there will appear a moment of restoring force (Fig.1): M = FREST×a = mga×sinα, (10) here m mass of a pendulum, a distance from the pivot point to center of gravity C of the pendulum, α small enough angle of deflection from equilibrium. The moment equation gives: M = Jε, (11) here mga sinα = Jε,
where J moment of inertia of the physical pendulum. Moment of inertia J is a physical analog of the mass of a rotating rigid body. For example, moment of inertia of the rotating point mass m apart on distance l from an axis is J=m×l2. (12) Then SI measurement units for moment of inertia is kilogram-square meter [kg×m2]. We note that such oscillating point mass m on weightless suspension of length l is being termed as simple (mathematic) pendulum. As α is small we can replace sinα by α in moment equation(10): from here we obtain differential equation of oscillations of physical pendulum:
Thus, oscillatory motion of physical pendulum is being described by the homogeneous second order differential equation. General solution for this differential equation will be equation of oscillations of physical pendulum:
α = αm cos(ω0t+φ0) (14)
Coefficient near α in (12) is squared cyclic eigenfrequency ω0, then
Taking in to account (8) well have a eigenperiod of the physical pendulum
In special case (12), for simple (mathematic) pendulum
Comparison of (16) and (17) shows that it is possible to pick such simple (mathematic) pendulum with length
which will have same period as a given physical has. Such length leq is called equivalent length of physical pendulum. Moment of inertia of physical pendulum we can determine using formula (14):
3 Description of laboratory research facility and methodology of measurements Devices and outfits: console with a pendulum, millimetre scaled ruler, stopwatch. In a given work we observe natural oscillations of physical pendulum. Such pendulum consists from a metallic rod, suspended by one of its ends and free to rotate in a vertical plane. Mass of a pendulum is indicated on a metallic rod in the form of numerical imprint. Length of a pendulum is being measured by a ruler once, but with pinpoint accuracy (important!). Instrumental accuracy 0,001m. Use small, about 3O 5O, deflections of a pendulum from its equilibrium state to make it oscillate. Only in this case oscillations will be harmonic. For small angle deflection α it is possible to calculate value of amplitude via an approximate equation: A= lsinα ≈ lα here l length of a pendulum. Direct measurements of period. The period is a small quantity, then for increasing an accuracy of its determination it is possible to measure time of 10 oscillations. When pendulum appears in one of its edge positions start stopwatch and count 10 complete oscillations (cycles). Use 0.01 precision when calculating average value of period. From average value of period it is possible to calculate a cyclic frequency of oscillations. From initial position according (4) and (4a) it is possible to calculate initial phase of oscillations and write equation of oscillations of pendulum with numerical coefficients A,ω0, φ0. Indirect measurement of moment of inertia. A task for students will be determination of moment of inertia of a given physical pendulum using its oscillations. Center of gravity of uniform rod is on the half of its length, so ΰ = l/2 . (21) Substituting (21) in (19) it is possible to obtain an experimental value of moment of inertia:
Free fall acceleration is 9.81 m/s2. From theoretical mechanics it is possible to calculate a theoretical value of moment of inertia:
Data processing
For representation of the result of direct measurements of quantity x it is necessary: 1) Obtain the sequence of measured values x1, x2, x3, ..., xn and write result of these n measurements in a second column of Table of measurements. In a first column of Table of measurements write an ordinal number of measurement. 2) Calculate the average value of measurand: 3) Find an abmodality each measurement and write result in a third column of Table of measurements:
4) Square each abmodality in a fourth column of Table of measurements and summarize them:
5) Find a statistical absolute error DxST of measurements from Students equation:
where a confidence probability; n number of measurements; ta;n Students coefficient. 6) If it is not identified an absolute instrumental error DxDEV on measuring tool, it is necessary to find a device absolute error of measurements from accuracy class b of electrical measuring instrument:
where υmax grid limit. 7) Find a total absolute error of measurements Dx = 7) Calculate relative error of measurements:
8) Final result should be represented by a confidence interval and relative error:
For representation of the result of indirect measuringof quantity y it is necessary: 1) Calculate the average value of measurand <y> by formula from average values of known quantities <a>, <b>, <c>, for example:
2) Calculate relative error of measurand dy from relative errors of known quantities da , db , dc by formula that should be gained accordingly to this example:
where Da, Db, Dc absolute errors of known quantities; <a>, <b>, <c> its average values. 3) Find an absolute error of measurand Dy =<y>×dy . (34)
4) Final result should be represented by a confidence interval and relative error:
Date: 2015-12-24; view: 1060
|
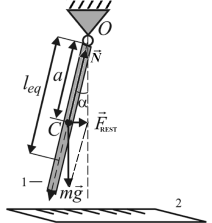 Figure 1 Restoring force of physical pendulum
Figure 1 Restoring force of physical pendulum
 angular acceleration, so
angular acceleration, so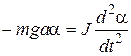 ,
,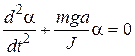 or
or 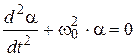 (13)
(13)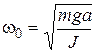 . (15)
. (15)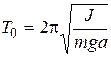 (16)
(16) and the eigenperiod will be
and the eigenperiod will be . (17)
. (17)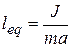 , (18)
, (18)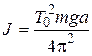 . (19)
. (19)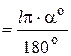 , (20)
, (20) . (22)
. (22)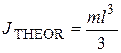 . (23)
. (23) . (24)
. (24) ;
; 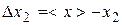 ; ... ;
; ... ;  . (25)
. (25)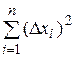
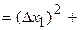
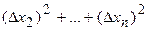 . (26)
. (26)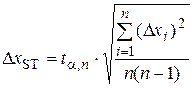 . (27)
. (27)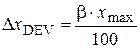 , (28)
, (28) (29)
(29)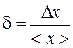 . (30)
. (30)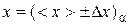 = (
±
)0.95;
= (
±
)0.95; 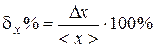 =
%. (31)
=
%. (31) . (32)
. (32) , (33)
, (33)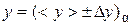 = (
±
)0.95;
= (
±
)0.95; 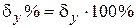 =
%. (35)
=
%. (35)