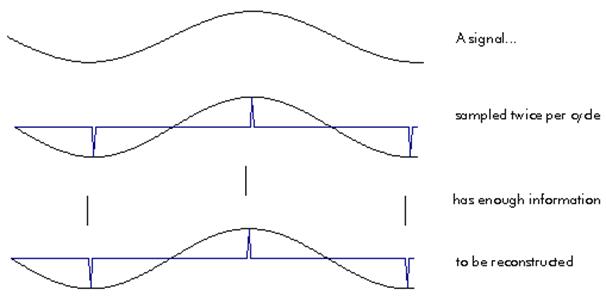
Nyquist's Signal Sampling Theory

In the late 1920s, the only technology to preserve musical recordings was to copy sound waves in wax. Harry Nyquist, an AT&T scientist, thought there was a better way. He wrote a landmark paper (Nyquist, Harry, "Certain topics in Telegraph Transmission Theory," published in 1928) describing the criteria for what we know today as sampled data systems. Nyquist taught us that for periodic functions, if you sampled at a rate that was at least twice as fast as the signal of interest, then no information (data) would be lost upon reconstruction. And since Fourier had already shown that all alternating signals are made up of nothing more than a sum of harmonically related sine and cosine waves2, then audio signals are periodic functions and can be sampled without lost of information following Nyquist's instructions. This became known as the Nyquist frequency, which is the highest frequency that may be accurately sampled, and is one-half of the sampling frequency.

Harry Nyquist (1920's) showed that to distinguish unambiguously between all signal frequency components we must sample at least twice the frequency of the highest frequency component, Figure 1.

Figure 1: In the diagram, the high frequency signal is sampled twice every cycle. If we draw a smooth connecting line between the samples, the resulting curve looks like the original signal. This avoids aliasing3. The highest signal frequency allowed for a given sample rate is called the Nyquist frequency.

Harry Nyquist thought of a way to take an analog signal (such as voice) and code it (just like with the Morse code) using ones (1) and zeros (0). For this, he invented something called a "CODEC" or coder-decoder. This thing that today is the size of a fingernail (a microchip) measures the input analog signal, codes the result of the measurement and sends this code down the telephone lines and trunks. It does so often enough so its peer at the other end of the line can reconstruct the voice signal almost as good as it was at the calling side. N. Erd calls the measuring of the signal "sampling." Good old Harry Nyquist also recommended that the number of samples per second for a good representation of the signal has to be twice as big as the number of Hertz of the fastest sine wave contained in the analog signal. Since the telephone only allows 4 kHz through the phone line, sampling for voice is done 8000 times per second.

Nyquist Theorem

Signal Sampling Theory was an exercise in frustration4 for Nyquist, since it needed 30,000 samples a second to make it work, and no system at that time could measure, record, store and reread that much information that quickly. He had to wait for computers, binary language, transistors and integrated circuits - 60 years of technological progress - to make digital recording and playback a reality.

The sampling theorem states that for a limited bandwidth (band-limited) signal with maximum frequency f_max , the equally spaced sampling frequency f_s must be greater than twice of the maximum frequency f_max, i.e.,

f_s > 2·f_max

in order to have the signal be uniquely reconstructed without aliasing. The frequency 2·f_max is called the Nyquist sampling rate. Half of this value, f_max, is sometimes called the Nyquist frequency. The sampling theorem is considered to have been articulated by Nyquist in 1928 and mathematically proven by Shannon in 1949. Some books use the term "Nyquist Sampling Theorem", and others use "Shannon Sampling Theorem". They are in fact the same sampling theorem.

The sampling theorem clearly states what the sampling rate should be for a given range of frequencies. In practice, however, the range of frequencies needed to faithfully record an analog signal is not always known beforehand. Nevertheless, engineers often can define the frequency range of interest. As a result, analog filters are sometimes used to remove frequency components outside the frequency range of interest before the signal is sampled. For example, the human ear can detect sound across the frequency range of 20 Hz to 20 kHz.

According to the sampling theorem, one should sample sound signals at least at 40 kHz in order for the reconstructed sound signal to be acceptable to the human ear. Components higher than 20 kHz cannot be detected, but they can still pollute the sampled signal through aliasing. Therefore, frequency components above 20 kHz are removed from the sound signal before sampling by a band-pass or low-pass analog filter. Practically speaking, the sampling rate is typically set at 44 kHz (rather than 40 kHz) in order to avoid signal contamination from the filter roll off.

What if an engineer is interested in sampling a mechanical signal across ALL frequencies? Most mechanical signals have frequencies limited to below 100 kHz. Therefore, using a 200 kHz sampling rate should satisfy most mechanical engineering applications. The price for such a high sampling rate will be the huge amount of sample data to be stored and processed. Note that this limit should NOT be applied to electric engineering, where signals can contain much higher frequencies!

Graphically, if the sampling rate is sufficiently high, i.e., greater than the Nyquist rate, there will be no overlapped frequency components in the frequency domain. A "cleaner" signal can be obtained to reconstruct the original signal. This argument is shown graphically in the frequency-domain schematic.

Date: 2015-12-24; view: 1033