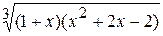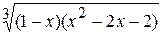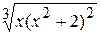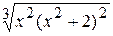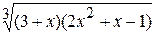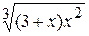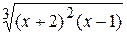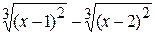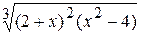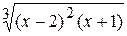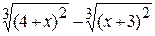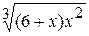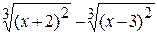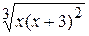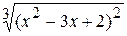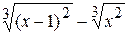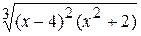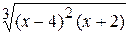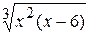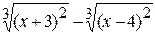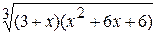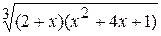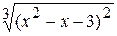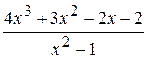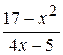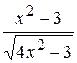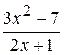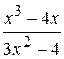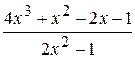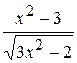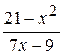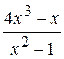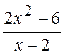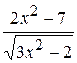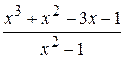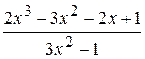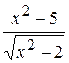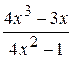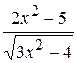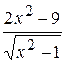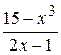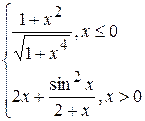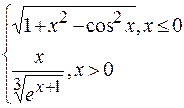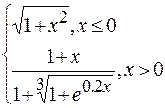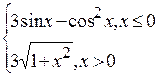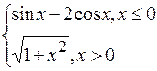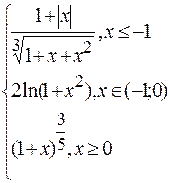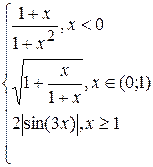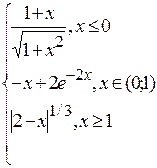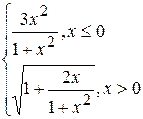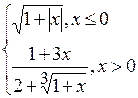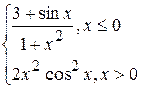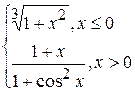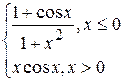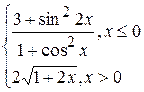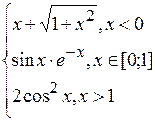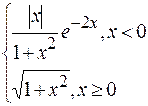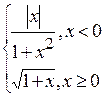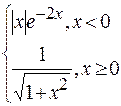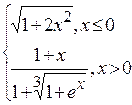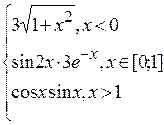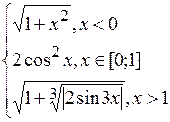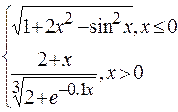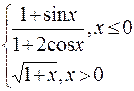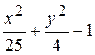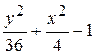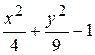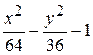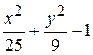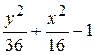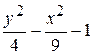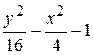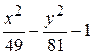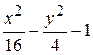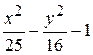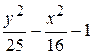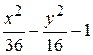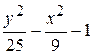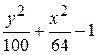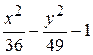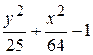CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Travail pratique ¹ 156.2.15.1 Création des graphiques de fonctions Objectif de travail: réception de l’expérience de la création des graphiques au milieu MS Excel. Il est commode de comprendre le processus de création d’un qraphique de fonction sur exemple. Exemple 1. Il faut créer le qraphique de la fonction La succession des opérations est suivante: 1. calcul de la fonction posée. Cet étape est realisé comme suit: – faire entrer dans la cellule A1première valeur d’argument x (–5); – faire entrer dans la cellule A2deuzième valeur d’argument x (– 4,5); – sélectionner cellules A1 et A2; – glisser la souris en appuyant le bouton gauche le long de colonne jusque la valeur finale de x qui s’affiche (A21); – créer la formule =(A1^2*(A1+3))^(1/3) dans la cellule B1; –copier cette formuledans les cellulesÂ2:Â21. 2. La création d’un qraphique. Cette création s’effectue à l’aide d’Assistant Graphique. L’étape de création est réalisé par les actions suivantes: – sélectionner la plage de cellules Â1:Â21; –cliquer sur l’icône fx de la barre d’outils; La boîte de dialogue de 1– er étape s’affiche; – sélecter le graphique du format courbes et puis l’échantillon de sous–type. On recommande de choisir le qraphique présentée par la famille de points liés par les segments; – cliquer sur le bouton Äàëåå (Suivant). Le passage en deuxième étape s’effectue; – marquer l’axe d’abssis par les valeurs de l’argument x; – cliquer sur le bouton Äàëåå(Suivant). Le passage en troisième étape s’effectue; – choisir lo nom de graphique, nom des axes des ordonnées, épaisseurs de lignes, la couleur de fond et celle de graphique (fig. 6.42); – cliquer sur le bouton Äàëåå(Suivant). Le passage en qutrième étape s’effectue; – choisir l‘endroit de graphique; – cliquer sur le bouton Ãîòîâî (Fin).
Fig. 6.42 Exemple 2. Il faut créer le qraphique de la fonction
Fig. 6.43 Le processus de création du graphique est le même qu’au –dessus. Mais ici il faut faire attention sur la zone de définition de la fonction. En analysant l’expréssion mathématique de la fonction on peut conclure que la fonction n’est pas déterminée en cas quand le dénominateur est null. C’est possible quand x = – 2. Fig. 6.43 illustre cette situation. L’ensemble des valeurs de l’argument x exclut la valeur –2. Exemple 3. Il faut créer le graphique de la fonction
Cette fonction est déterminée si x2 – 1 >= 0. À son tour c’est possible quand
La détermination de l’argument x il faut faire en deux étapes: – pour la zone de – 5 jusqu’à – 1 et – pour la zone de 1 jusqu’à 5. Toutes les valeurs Exemple 4. Il faut créer le graphique de la fonction
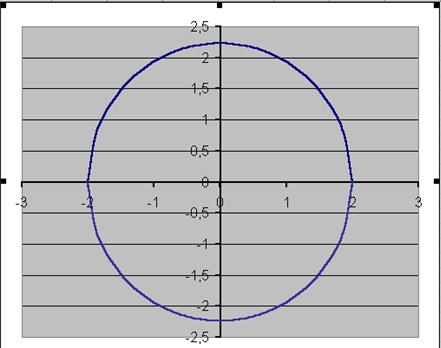
Fig. 6.44 Le calcul des valeurs de la fonction posée s’effectu avec l’utilisation de la fonction de bibliothèque MS Excel ÅÑËÈ (si). Par exemple, la valeur initiale de l’argument x = – 2 est installée dans la cellule À7 (fig.6.44). La formule de calcul de la fonction posée est disposée dans la cellule Â7: =ÅÑËÈ(A7<0;1+A7;ÅÑËÈ(A7>=1;A7^2;EXP(A7))). En correspondance aux valeurs obtenues (cellules B7:B27)le graphique est créé (fig.8.3). Exemple 5. Il faut créer le graphique de la fonction 4y2 + 5x2 – 20 = 0 si x est variée de sa valeur initiale –2 jusqu’à sa valeur finale 2 avec le pas 0,1. Il convient de noter que la fonction posée f(x,y)=0décritunecourbe qui s’appeleellipse. Cela peut être démontré par les opérations élémentaires:
Cette expréssion En tenant compte que l’équation est présentée sous la forme nonévidente pour la création du graphique il la faut resoudre par rapport à la variable y:
Après toutes les conversions on peut voir que la courbe f(x,y) peut être présentée en créant le graphique de deux fonctions
dans la même surface des ordonnées. Avant de création du graphique il faut déterminer la zone de valeurs des fonctions
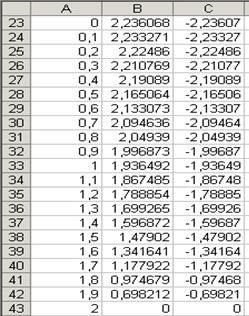
Après cette opération on peut commencer à créer un graphique. Avec cela il faut: – faire entrer les valeurs d’argument dans les cellules À3:À43. – composer la formule pour le calcul de fonction =ÊÎÐÅÍÜ(20-5*$A3^2)/2 et la formule pour le calcul de fonction = – ÊÎÐÅÍÜ(20-5*$A3^2)/2; – copier ces formules dans les cellules Â43 et Ñ43en correspondance(fig. 6.45); – sélectionner le diapason de cellules À3:Ñ43; –créer les graphiques de fonctions
Fig. 6.45
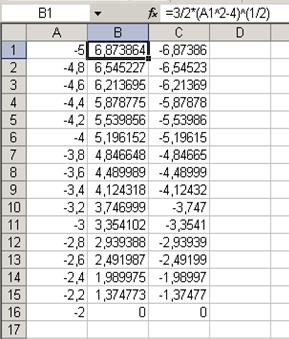
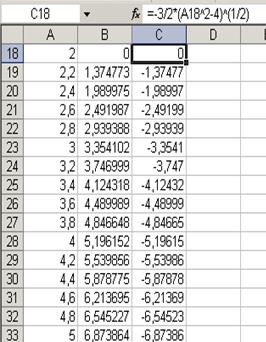
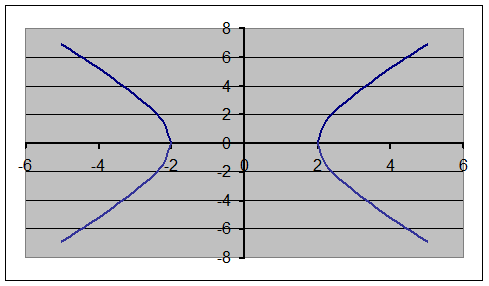
Fig. 6.46 Exemple 6. Il faut créer un graphique de la fonction présentée sous la forme nonévidente: Cette équation décrit la ligne qui s’appele hyperbole. Avant de créer le graphique il faut tout d’abord resoudre cette équation par rapport à la variable y:
La zone de définition des fonctions
La recherche analytique faites montre que les arguments de la fonction pour le graphique créé doivent être présentés en deux zones. Dans la zone –2 … 2 la fonction n’est pas déterminée. (voir exemples 2 et 3). La détermination des valeurs d’arguments de fonctions
Fig. 6.47
Fig. 6.48. 6.2.15.2 Énoncé du problème Il faut créer les graphiques des fonctions d’après les variantes présentées au–dessous. Variantes Problème 1.
Problème 2.
Problème 3.
Problème 4.
6.2.15.4 Questions de contrôle 1.Quelle est l’ordrede la créationdu graphique de la fonction qui a la zone indéfinie? 2.Quelle est la propriété de la création du graphique d’une ellipse? 3.Quelle est la propriété de la création du graphique d’une fonction hiperbolique? 4. Donnez la définition de la zone indéfini d’une fonction.
Date: 2015-12-24; view: 715
|
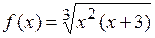 si x est variée de sa valeur initiale –5 jusqu’à sa valeur finale 5 avec le pas 0,5.
si x est variée de sa valeur initiale –5 jusqu’à sa valeur finale 5 avec le pas 0,5.
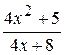 si x est variée de sa valeur initiale –5 jusqu’à sa valeur finale 5 avec un pas 0,2.
si x est variée de sa valeur initiale –5 jusqu’à sa valeur finale 5 avec un pas 0,2.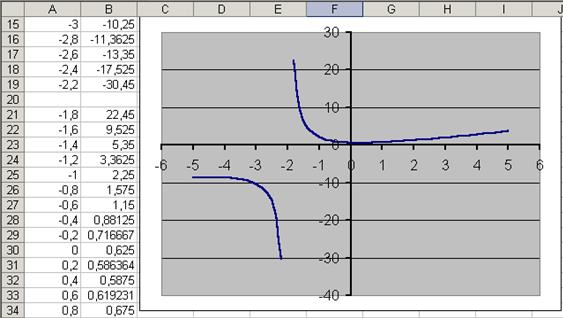
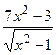 si x est variée de sa valeur initiale –5 jusqu’à sa valeur finale 5 avec le pas 0,2.
si x est variée de sa valeur initiale –5 jusqu’à sa valeur finale 5 avec le pas 0,2. .
.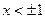 doivent être exclues.
doivent être exclues. si x est variée de sa valeur initiale –2 jusqu’à sa valeur finale 2 avec le pas 0,1.
si x est variée de sa valeur initiale –2 jusqu’à sa valeur finale 2 avec le pas 0,1.
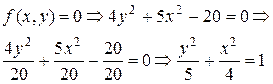 .
. est l’équation d’ellipse.
est l’équation d’ellipse.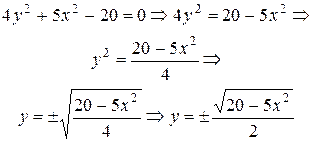
 è
è 
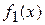 et
et  . Cette zone est déterminée comme suit:
. Cette zone est déterminée comme suit: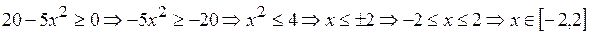

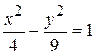 , si x est variée de sa valeur initiale –5 jusqu’à sa valeur finale 5avec le pas 0,2.
, si x est variée de sa valeur initiale –5 jusqu’à sa valeur finale 5avec le pas 0,2.
 .
.