
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Vérification du calcul des racinesb = . . . c = . . . Òàbleau 5.8
5.9.2 Généralités et recommandations pour l`exécution du travail On appele le nombre complexe un nombre de la vue α + βi qui se compose de deux parties écrites toujours côte à côte. À la différence du nombre réel qui est présenté sous forme d`un point sur l`axe réel le nombre complexe se représente comme un point sur la surface de coordonnées rectangulaires ( fig. 5.1 ). La partie α est appelée la partie réele du nombre complexe. Elle correspond à la projection du vecteur sur l`axe d`abcisse nommée réele. La partie βi est appelée la partie imaginaire. Elle correspond à la projection du vecteur sur l`axe d`ordonnée nommée imaginaire . L`axe d`abcisse est marquée par la signe + , l`axe d`ordonnée est marquée par le symbole i ou j . Le multiplicateur i de la partie imaginaire est égale à En cas particulier n`importe quel nombre réel peut être présenté comme le nombre complexe avec la partie imaginaire égale à zéro. Par exemple, c + 0i où le nombre réel est présenté sous forme complexe. Il est résulte que le nombre réel c peut être présenté par un vecteur qui coïncide avec l`axe d`abcisse .Ce vecteur est tracé entre l`origine des coordonnées et le point C qui correspond à la valeur du nombre. Le longueur de ce vecteur est égale à la valeur du nombre C. ( fig. 5.1). En face des nombres réels on distingue les nombres purement imaginaires comme le deuxième cas particuliér du nombre complexe. Dans ce cas la partie réele est égale à zéro. Par exemple, 0 + di ( fig. 5.1 ). Il est à noter que la signe écrite entre la partie réelle et celle imaginaire ne signifie pas l`opération de soustraction ou bien d`addition entre ces parties. Cette signe se rapporte à la partie imaginaire qui est écrite toujours après la partie réele et à côte d`elle. Les exemples des nombres complexes sont les suivantes 5 + 2.8i , 7.2 12i , -1 + 0i , 0 + 5i . Les deux derniers nombres se représentent comformement au nombre purrement réel et celui imaginaire. La forme plus simple de l`écriture de ces nombres est -1 et 5i . La forme de l`écriture examinée des nombres complexes est appelée la forme a l g e b r i q u e . La plus vaste forme pour la présentation des nombres complexes est la forme d e p u i s s a n c e qui est utilisée en mathématique , par exemple, La forme algebrique est commode pour l`addition et la soustraction des nombres complexes, la forme de puissance pour la multiplication et la division. En cas d`obtention du discriminent négatif lors du calcul des racines de l`équation quadratique les derniers prendront la forme complexe conjuguée. Les nombres de forme complexe conjuguée se distinguent seulement par le signe de la partie imaginaire, par exemple, 3 + 4i et 3 4i. La racine carrée du nombre négatif est le nombre purrement imaginaire, par exemple,
Le langage C++ a la bibliothèque des fonctions prédéfinies pour le traitement des nombres complexes. Elle se trouve dans le fichier de bibliothèque complex.h ( appendice 1 ). Afin de l`utiliser, il faut prévoir dans le programme la directive # include < complex.h > L`opération d`affectation avec les nombres complexes a la forme suivante H = ( -1, 3) ; Elle montre que la variable du type complexe h obtient sa valeur -1 + 3i . La partie réelle du nombre Les opérations arithmétiques avec des nombres complexes sont les mêmes que celles qui sont utilisées avec les nombres réels. Par exemple, le résultat de la réalisation du fragment suivant du programme complex h1 = (2,-3.5) , h2 = (-1,5) ; complex h = h1 + h2 ; . . . . . . . . . . . . . . . . . . . cout<<h ; . . . . . . . . . . . . . . . . . . . est ( 1 , 1.5 ). Cela signifie que la variable h obtient sa valeur 1 + 1.5i . En tenant compte de la spécification de l`affichage des nombres complexes on a besoin de composer la fonction spéciale pour l`affichage des nombres complexes sous forme traditionnelle (algebrique ). Les fonctions principales du fichier complex.h sont présentées dans l`appendice 2. Lors de la composition du programme on recommande déclarer les nombres complexes comme constantes et utiliser leurs identificateurs dans les expréssions .
5.9.3 Questions de contrôle et devoirs
1. Ècrivez le nombre complexe sous forme algebrique et de puissance dont la partie réelle est égale à 3 et celle imaginaire est égale à 3 . 2.Comment déclare t on la variable complexe et la constante complexe ? Donnez l`exemple. 3.Quelles opérations mathématiques peuvent être réalisées avec les nombres complexes ? 4.Enumérez et déchiffrez la destination des fonctions prédéfinies pour le traitement des nombres complexes nécessaires pour la composition du programme selon la variante donnée.
Date: 2015-12-24; view: 866
|
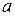
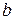
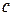




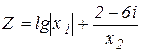




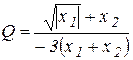
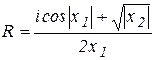
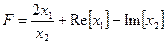
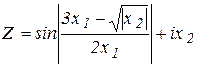

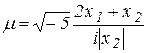
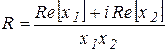

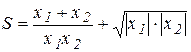
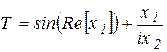


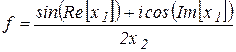

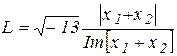


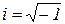 . Il est appelé l`unité imaginaire.
. Il est appelé l`unité imaginaire.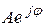 ( fig. 5.1). Ici
( fig. 5.1). Ici  est la valeur absolute du nombre complexe ou bien une a m p l i t u d e,
est la valeur absolute du nombre complexe ou bien une a m p l i t u d e,  est un a g u m e n t ou p h a s e du nombre complexe.
est un a g u m e n t ou p h a s e du nombre complexe. .
. , imaginaire
, imaginaire 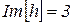 . La valeur absolute
. La valeur absolute 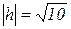 ,argument
,argument  .
.