
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
The derivative of the function. Geometric and mechanical meaning. Table of derivatives. The differential of a function
Theoretical questions: 1.Definition of derivative. 2. The geometric meaning of derivative. 3. The basic rules of finding derivatives. 4. Derivatives of the basic elementary functions.5. Derivative of composite functions, implicit functions, the functions specified parametrically, the method of logarithmic differentiation. 6. Application of the differential to approximate calculations. Classroom assignments:
1. Find derivatives of following functions: 1) 4) 7) 11) 2. Calculate derivatives of following functions defined implicitly: 1. 3. 3. Calculate derivatives of following functions defined parametrically: 1. 4. Using the method of logarithmic differentiation calculate derivatives of following functions: 1. 4. 5. Find differential of functions: 1. 4. 6. Find the approximate value: 1.
Homework: Theoretical material: L'Hopital's rule. Investigation of the function. Extremum of the function. Convexity, concavity and inflection points. Asymptote. Solve problems: 1. Find derivatives of the following functions applying the formulas and rules of differentiation: à) â) ä) 2. Calculate derivatives of functions: 1. 4. 3. Show that the function 4. Find differentials of functions: à) 5. Using a differential calculate approximately: à) 6. For function
PRACTICAL CLASS ¹ 7-8. Rolle's theorem, Lagrange, Cauchy. L'Hopital's rule. Investigation of the function. Extremum of the function. Necessary and sufficient conditions for the existence of an extremum. Convexity, concavity and inflection points. Asymptote. The overall study of design features
Theoretical questions: 1.L’Hospital’s Rule; 2.Monotonic conditions. Extremum of function; 3.Convexity and concavity. Point of inflection; 4.Àsymptotes; 5.Scheme of investigation of function and charting.
Classroom assignments: 1. Find the limits using L'Hospital's rule: 1. 2. Conduct a complete investigation of the functions and construct their graphs: 1. 3. Describe the concavity of the graph of 4.Find 5.Find the domain and all asymptotes of the following function: 6. Find the maximum and minimum values of Homework: Theoretical material: Antiderivative and indefinite integral. Solve problems: 1. Find the limits using L'Hospital's rule: 1. 2. Conduct a complete investigation of the functions and construct their graphs: 1. 3. Find the domain and all asymptotes of the following function: 4. Find the domain and all asymptotes of the following function: 5. Find the maximum and minimum values of 6. Find the maximum and minimum values of PRACTICAL CLASS ¹ 6.
Date: 2015-01-02; view: 1726 |
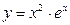 ; 2)
; 2)  ; 3)
; 3) 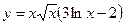 ;
; ; 5)
; 5) 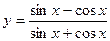 ; 6)
; 6)  ;
;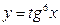 ; 8)
; 8) 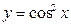 ; 9)
; 9) 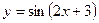 ; 10)
; 10) 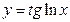 ;
; ; 12)
; 12) 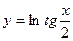 ; 13)
; 13) 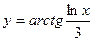 .
.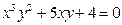 2.
2. 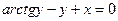
 4.
4. 
 2.
2. 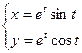 3.
3. 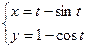 4.
4. 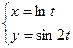
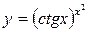 2.
2.  3.
3. 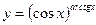
 5.
5. 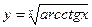 6.
6. 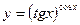
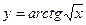 2.
2. 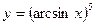 3.
3. 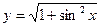
 5.
5. 
 2.
2. 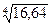 3.
3. 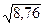 4.
4. 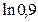 5.
5. 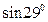 6.
6. 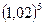 7.
7. 
 ; á)
; á) 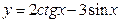 ;
;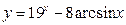 ; ã)
; ã) 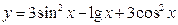 ;
;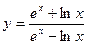 ; å)
; å) 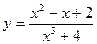 .
. 2.
2.  3.
3. 
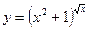 5.
5. 
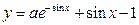 satisfies the relation
satisfies the relation 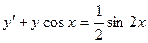 .
.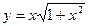 ; á)
; á) 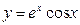 â)
â) 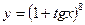
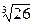 ; á)
; á) 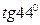
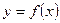 à)
à)  á)
á) 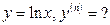
 2.
2. 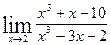 3.
3.  4.
4. 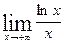 5.
5. 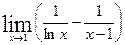 6.
6.  7.
7. 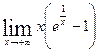 8.
8. 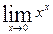 9.
9. 
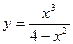 2.
2. 
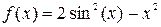 for
for  .
.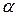 and
and 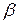 so that the function
so that the function 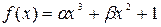 has a point of inflection at
has a point of inflection at 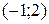 .
.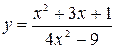 .
.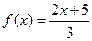 on the interval [0, 5].
on the interval [0, 5].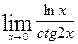 2.
2. 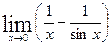 3.
3.  4.
4. 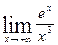
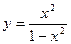 2.
2. 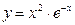 .
.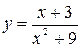 .
.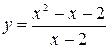 .
. on the interval [-2, 1].
on the interval [-2, 1].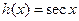 on the interval
on the interval  .
.