
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Type 5.Other rational expressions with the irrational function 1. If 2. If 3. If 4. If Frequently occuring integrals of irrational functions are: Taking the factor
3. Integration of TRIGONOMETRIC functions
1. Given an integral 2. If 3. If If 4. 5. For integrals
6.
Date: 2015-01-02; view: 1154
|
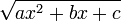
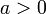 , we can use
, we can use 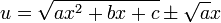 .
. , we can use
, we can use  .
.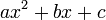 can be factored as
can be factored as 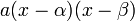 , we can use
, we can use 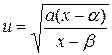 .
.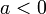 and
and 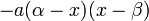 , we can use
, we can use 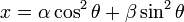
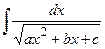 , where
, where 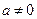 and
and 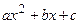 is possitive on an interval. We can exclude the case, that the polynomial
is possitive on an interval. We can exclude the case, that the polynomial 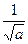 (if
(if 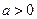 ) or
) or 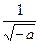 (if
(if 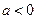 ) we reduce the integral to the form
) we reduce the integral to the form 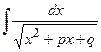 or
or 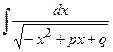 , leading (by means of substitution) to the integrals:
, leading (by means of substitution) to the integrals: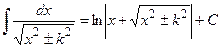 or
or 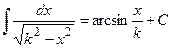 , respectively.
, respectively.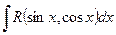 , i.e. the integrand is a rational function in terms of
, i.e. the integrand is a rational function in terms of 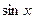 and
and 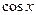 . By the substitution
. By the substitution 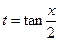 the integral is reduced to an integral of a rational function. If
the integral is reduced to an integral of a rational function. If 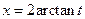 ,
, 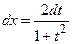 ,
,  and
and 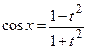 .
.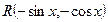 =
= 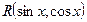 , then
, then 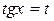 .
. = -
= - 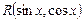 , then
, then 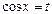 .
.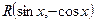 =-
=- 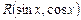 , then
, then 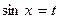 .
.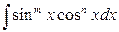 , ò and ï – even non-negative integers, then
, ò and ï – even non-negative integers, then  ,
, 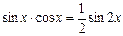 .
.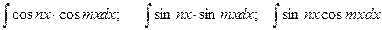 we use following formulas:
we use following formulas: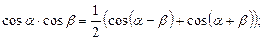
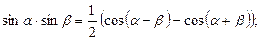
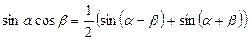
 , then
, then  and
and 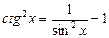 .
.