The eccentricity and directrix of an ellipse. Consider the focal radii of an ellipse

; .

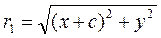By definition, we have

.

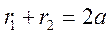Consider the difference of squares

;

,

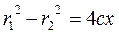or .

y

d₁ М(х;у) d₂

r₁ r₂

F₁(–c;0) 0 F₂(c;0) x

x=–l x=l

to determine the focal radii, we solve the system of equations

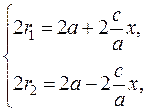or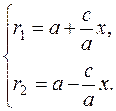

Definition. The ratio of distances between the foci to the sum of focal radii is called eccentricity:

.

If the distance between the foci is less than 2а, then the eccentricity is
.

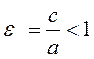Thus, the focal radii of the ellipse are

,

.

Definition. The directrix of an ellipse is the straight line parallel to the y-axis such that the ratio of the focal radius to the distance from an ellipse point to it is constant and equal the eccentricity.

Let us draw two straight lines x=–l and x=l parallel to the y-axis and find l such that the ratio of the focal radius to the distance from a point М to this straight line is constant and equals the eccentricity:

.

Substituting the distance and the focal radius, we obtain

.

The ratio is equal to the eccentricity when 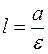, i.e., 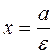is the directrix. By analogy, we obtain equations of the directrices:

; ,

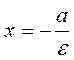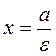where .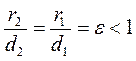

Date: 2015-01-02; view: 838