The Gauss-Jordan Method

Consider the Gauss method in the case where the number of equations coincides with that of unknowns:

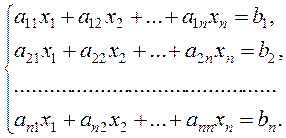(6)

Suppose that а₁₁ 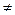0; let us divide the first equation by this coefficient:

. (*)

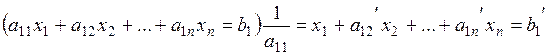Multiplying the resulting equation by –а₂₁ and adding it to the second equation of system (6), we obtain

.

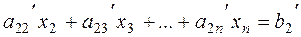Similarly, multiplying equation (*) by –а_n1 and adding it to the last equation of system (6), we obtain

.

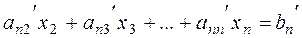At the end, we obtain the new system of equations with n–1 unknowns:

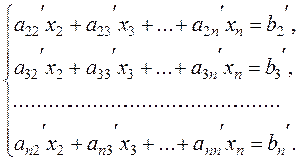(7)

System (7) is obtained from system (6) by applying linear transformations of equations; hence this system is equivalent to (6), i.e., any solution of system (7) is a solution of the initial system of equations.

To get rid of х₂ in the third, the forth, …, nth-equation, we multiply the second equation of system (7) by 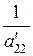and, multiplying this equation by the negative coefficients of х₂ and summing them, obtain

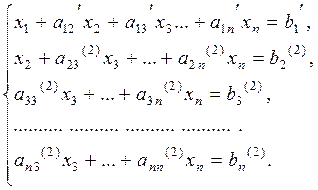
Performing this procedure n times, we reduce the system of equations to the diagonal form

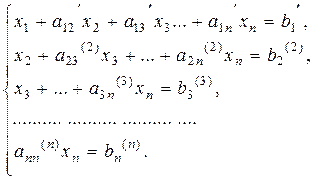
We determine х_n from the last equation, substitute it in the preceding equation and obtain x_n-1, and so on; going up, we determine х₁ from the first equation. This is the classical Gauss method.

Consider the system of m equations with n unknowns

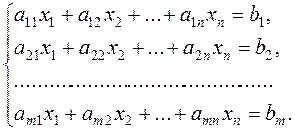(8)

Definition. The matrix composed of the coefficients of system (8) is called the principal matrix of this system:

.

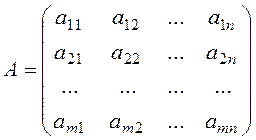Adding the column of free terms of system (8) to this matrix, we obtain the augmented matrix

.

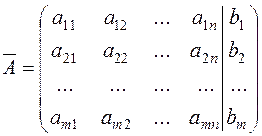The following linear operations on the rows of such a matrix are allowed:

- permutation of rows;

- multiplication of a row by some number and adding it to another row;

- permutation of columns (but we must remember to which unknowns they correspond);

- no operations on columns are allowed (columns cannot be multiplied by numbers, summed, etc).

The Gauss-Jordan method consists in reducing (by linear operation on rows) the principal matrix to the identity matrix, i.e., to the form

.

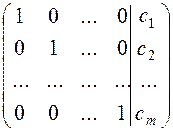If the columns were not interchanged, the solution of the system of linear equations is

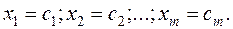
Examples. Solve the following system of equations by the Gauss-Jordan method:

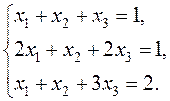
We compose the augmented matrix of the system and, applying linear combinations of rows, reduce the principal matrix to the identity:

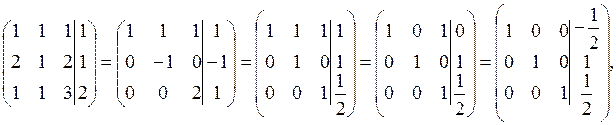
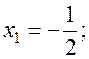
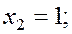
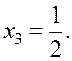
Date: 2015-01-02; view: 917