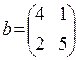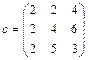CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Laboratory work ¹14.Bit-by-bit addition, subtraction, multiplication and division of two massifs. Decision of system of the linear equations. Objective: To learn the elementary operations over massifs, to use built-in functions for work with matrixes
Often during the work with tables there is a need to apply the same operation to the whole range of cells or to make calculations for the formulas depending on a big data file. The massif in a spreadsheet of Excel is understood as the rectangular range of formulas or values which the program processes as uniform group. Multiplication of the massif by number. As the first example of simple operation over massifs we will consider multiplication of the massif located in the range of A1:B2 on number 5. For this purpose allocate on a work sheet area, the same size, as well as an array multiplicand, for example D1:E2. Now, without canceling allocation, enter a formula. For this purpose install the cursor in a line of formulas and finish input not as usual, <enter> key pressing, and simultaneous pressing of the keys <ctrl>, <shift>, <enter>. Thus you report to the program about need to execute operation over the massif. At this MS Excel will take a formula in a line of formulas in braces and will make demanded calculations with elements of the massif and will conclude a formula in a line of formulas in braces: { = A1:B2*5 }. Remember that input of a formula begins with the sign "=" During the work with massifs the formula affects all cells of range. It is impossible to change separate cells in formula operands. In MS Excel there are, for example, following special functions for work with matrixes: enter, shift, ctrl
In all cases during the work with matrixes before input of a formula it is necessary to allocate area on a work sheet where the result of calculations will be output. JOB 1. To calculate an array C on a formula: C=A+B where massifs have an appearance
1.1 Enter arrays A and B into A1:C2, D1:F2 ranges 1.2 Allocate on a work sheet the range of A5:B6 in which the result of bit-by-bit addition of two massifs will be placed. 1.3 In a line of formulas enter a formula =B1:C2+E1:F2. Finish input by simultaneous pressing of a combination of the Ctrl, Shift and Enter keys. Pay attention to braces in line the formulas which are forming after input of a formula.
JOB 2. To calculate an array C on a formula: C=A/B 2.1 Allocate on a work sheet the range of A8:B9 in which the result of bit-by-bit division of two massifs will be placed. 2.2 In a line of formulas enter a formula =B1:C2/E1:F2. Finish input by pressing of a combination of the Ctrl, Shift, Enter keys. Similarly calculate element-wise a difference, work of massifs. JOB 3. Calculate the massif which elements are equal to values of the cos function from the corresponding elements of a required array A
3.1. Enter an array A into A1:B2 range 3.2. Allocate on a work sheet the range of D4:E5 in which the result of calculation will be placed. 3.3. In a line of formulas enter a formula =cos (A1:B2). Finish input by pressing of combinations of the Ctrl+Shift+Enter keys.
JOB 4. Solve system of the linear equations: 8x1+3x2=4 2x1+7x2=2
4.1. We will write down this system in a matrix type of A*X=B where the A-matrix of coefficients has an appearance:
 – column of free members:
Õ – column of unknown:
Solution of this system has an appearance: X=A-1*B, where A-1 the return matrix to A 4.2. Enter basic data, as shown in Picture 15:
Picture 15
4.3. Allocate the range of F2:F3 into which the decision will be entered. In a line of formulas enter a formula, using the Master of functions: = =ÌÓÌÍÎÆ(ÌÎÁÐ(A2:B3);D2:D3). Finish input by simultaneous pressing of the Ctrl, Shift and Enter keys. 4.5 The decision of system of the equations is the vector
JOB 5. Solve system of the linear equations of A3*X=B where matrixes of A and B have an appearance:
The solution of this system is vector X=(A3)-1*B. For finding of a vector by X it is feasible the following actions: - enter elements of a matrix of A into the range of cells of A2:B4; - enter elements of a matrix of B into the range of cells of D2:D3; - allocate F2:F3 range where we will place elements of a vector of the solution in a line of formulas enter a formula: =ÌÓÌÍÎÆ(ÌÎÁÐ(ÌÓÌÍÎÆ(ÌÓÌÍÎÆ(A2:B3;A2:B3);A2:B3));D2:D3) and finish Finish input by pressing of combinations of the Ctrl, Shift è Enter. - in the range of cells of F2:F3 the solution of system of the equations will be found. JOB 6. Decision of system of the linear equations Kramer's Method. Calculation of a square form (the option is defined by the teacher) 1. Solve system of the linear equations Kramer's Method (table 42, a): 1.1. Using the function ÌÎÏÐÅÄ(),calculate determinant of a matrix And 1.2. In a matrix And replace the first column with values of a vector In and calculate determinant of the received matrix 1.3. Partial these two figures will be the first value of a vector X, i.e. õ1 1.4. Similarly calculate other values of a vector X 2. Calculate a square form z, (Table 42, b).
Table 42
JOB 7. Calculation of difficult expressions. Find value of the following expression (X – a vector from n of components, B and C – matrixes):
7.2 Enter elements of a matrix of B into the range of cells of B2:C3; 7.3 Enter elements of a matrix of C into the range of cells of D2:E3; 7.4 Allocate B6 cell where value of expression will be placed. In a line of formulas enter a formula and finish input by simultaneous pressing of the Ctrl, Shift and Enter keys: = (2*ÑÓÌÌ(A2:A4) + ÑÓÌÌ(B2:C3*D2:E3)^2)/(1+ÑÓÌÌ(A2:A4^2)). In a cell of B6 value S will be displayed Note: The same result can be received and without use of formulas of massifs, having entered into B6 cell a formula: =(2*ÑÓÌÌ(A2:A4)+ÑÓÌÌÏÐÎÈÇÂ(B2:C3;D2:E3)^2)/(1+ÑÓÌÌÊÂ(A2:A4)) Arguments which are massifs, have to have identical dimensions. The ÑÓÌÌÏÐÎÈÇ function () returns the sum of works of the corresponding elements of massifs. Syntax: ÑÓÌÌÏÐÎÈÇÂ(ìàññèâ1; ìàññèâ2; … ) The ÑÓÌÌÊ function () returns the sum of squares of arguments. Syntax: ÑÓÌÌÊ (÷èñëî1; ÷èñëî2; … ) JOB 8. The given matrixes are ÀandÂ, which have an appearance
Solve: • array A work on number 7; • sum and difference of arrays A and B; • bit-by-bit work and division of arrays A and B; • value of the sin function from each element of an array A;
JOB 9. Solve system of the linear equations: 2 x1+x2=3 4 x1+5 x2=2 JOB 10. 1. Find the return matrix to a matrix (A+V). Check result, having calculated work of an initial matrix and the return to it (the second column). 2. Solve system of the linear equations (A*X=B, A2*X=B, A3*X=B) with the method of the return matrix (the third column).
JOB 11. Find the value of following expression: 11.1.
X, Y –vectors from n components, A – matrix of mõm dimension, where n=4, m=2
11.2.
X, Y – vectors from n components, whereas, n=4
11.3. Find the value of difficult expression S, where à, x, y – vectors from n components, b and c – dimension matrixes (table 43).
Table 43.
Date: 2015-12-24; view: 1602
|


 á)
á) 



 á)
á)


 á)
á)

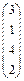








 7.1 Enter elements of a matrix of X into the range of cells of A2:A4;
7.1 Enter elements of a matrix of X into the range of cells of A2:A4;





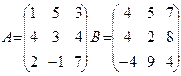


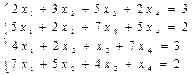
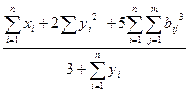 , where X= {1;2;7;4} Y= {1;7;2;3} B=
, where X= {1;2;7;4} Y= {1;7;2;3} B= 
 , where X= {7;5;7;4} Y= {2;4;2;3}
, where X= {7;5;7;4} Y= {2;4;2;3}
 ,
,