
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
I-Way: abc is equivalent to 2.2.Inequality problems Ardak Mirzahmetov Theorem 1. ( If Theorem 2.(
Theorem 3.(
Theorem 4. (
Theorem 5. (
Theorem 6.(
Theorem 7. (
Theorem 8. (Jensen
CHAPTER - 1 1.1.(a,b 1.2. (a,b>0) a+b 1.3. (a,b,c 1.4.(a,b,c 1.5. (a,b,c 1.6. (a,b,c 1.7. (a,b,c>0) (a+b+c)( 1.8. (a,b,c > 0) 1.9. (a,b,c 1.10. (a2+b2+c2=1) 1.11. (a,b 1.12. (a,b,c 1.13. (n 1.14. (a,b,c 1.15. (a,b,c 1.16. 1.17. 1.18. 1.19. 1.20. 1.21. (a,b,c>0 , a+b+c=1) 1.22. 1.23. 1.24. Compare: 1.25. Compare: 1.26. 1.27. (a,b,c are sides of a triangle) 1.28. (x+y=2, x , y ≥ 0) 1.29. (x, y > 0) 1.30. (-1 < x , y, z < 1) 1.31. (a, b, c ≥ 0, a+b+c=1) 1+9abc ≥ 4 1.32. ( 1.33. ( 1.34. ( 1.35. 1.36. Find the minimum value of 1.37. (a,b
CHAPTER - 2 2.1. (
2.2. (a,b,c 2.3. (a,b,c>0) a2 + b2+ c2 + 2.4. (a,b>0) 2.5. (ab=1) a2+b2 2.6. (a,b,c 2.7. (a,b,c,d>0) 2.8. (a 2.9. ( (1+2 2.10. (a,b,c>0 , a+b+c=1) (1+a)(1+b)(1+c) 2.11. (1+x 2.12. (a,b,c>0) ( 2.13. (a,b,c>0 , abc=1 ) 2.14. (0<a,b,c<1, a+b+c=2) 2.15. (a,b,c>0) abc 2.16. (a,b 2.17. (a,b,c>0) 2.18. (a,b,c>0 , a+b+c=1) 2.19. (a,b,c>0 , abc=1 ) 2.20. (a,b>0) 2.21. (a,b,c>0 , abc=1 ) 2.22. (x,y 2.23. (x 2.24. (a,b>0, a+b=1) 2.25. (a,b,c 2.26. (n 2.27. ( a,b 2.28. 2.29. (a,b,c>0 , abc=1 ) 2.30. 2.31. 2.32. 2.33. 2.34. 2.35. 2.36. (x+y+z >0) 2.37. (a,b,c >0) 2.38. (a,b,c>0 , abc=1 ) 2.39. 2.40. 2.41. 2.42. 2.43. 2.44. 2.45. 2.46. (0<x,y,z<1) x(1-y)+y(1-z)+z(1-x)<1 2.47. (a, b, c > 0) 2.48. (x+y+z+t=0, 2.49. 2.50. ( 2.51. 2.52. 2.53. (a,b,c are sides of a triangle) 2.54. 2.55.
SOLUTIONS CHAPTER - 1 1.1. 1.2. 1.3. 1.4. 1.5. 3(a2+b2+c2) ≥ (a+b+c)2 ⇔ (a- b)2+(b- c)2+(c- a)2 ≥ 0 1.6.By 1.2. 1.7.ByA.M. ( 1.8.A.M. 1.9.A.M.
1.10. By 1.3. 1= a2+b2 +c2
1.11. A.M. 1.12. A.M. Similarly 1.13. A.M. 1.14.(a-1)2+(b-2)2+(c-3)2 ≥ 0 1.15. By A. M. ≥ G.M.: a4+b4+ 1.16. By Cauchy’s inequality: 1.17. By Cauchy’s inequality: (3a+4b+12c)2≤(32+42+122)(a2+b2+c2)= =169(a2+b2+c2) ⇒ 3a+4b+12c ≤ 13∙ 1.18. By Cauchy’s inequality: (2x+3y)2=(2x+ ⇒ 1.19. By Cauchy’s inequality: 142≤(a+2b+3c)2≤(a2+b2+c2)(12+22+32)=(a2+b2+c2)14 ⇒ 14 ≤ a2+b2+c2 1.20. By Cauchy’s inequality: ( 1.21.. By Cauchy’s inequality:( 1.22. By Cauchy’s inequality: (a+b+c)2 ≤ (12+12+12)(a2+b2+c2)=9 ⇒a+b+c ≤ 3; By A. M. ≥ G.M.: 3 = a2+b2+c2 ≥ 3∙3 1.23. ad < bc ó ad < (a+d-c)c ó 0 < (c-d)(a-c) 1.24.For k < 1.25.1 3 Multiply them side by side. 1.26. 1.27. By triangle inequality a+b > c, ⇒ ac+bc > c2. Similarly ab+cb > b2, ab+ac > a2. Add them side by side . 1.28.
1.29.A.M-G.M.: 1.30.A.M-G.M.:
1.31.A.M-G.M.: 1.32.
1.33.
1.34. By A.M.
1.35. By A.M.
1.36.A.M. 1.37. a3+b3
CHAPTER - 2 2.1.By Cauchy’s inequality
2.2. By Schur’s inequality
a3+b3+c3+3abc 2.3.a2+b2+c2+
2.4.
2.5.A.M. = 2.6.A.M. 2.7.
2.8.
2.9.
2.10. A.M.
2.11.If If
II-solution. By mathematical induction. 2.12. A.M.
2.13. abc=1
2.14.1-a=x, 1-b=y, 1-c=z
I-Way: abc is equivalent to 2.2. II-way: Assume that a+b-c, b+c-a, c+a-b are positive and a+b-c=x , b+c-a=y, c+a-b=z 2.16.By A.M. Similarly 2.17.A.M. Similarly
Equality occurs when 2.18.. A.M .
2.19. let a = x2, b = y2 , c = z2,
( AM Add inequalities (1), (2) side by side. 2.20. it becomes 2.21. A.M. Similarly Similarly
2.22. 2.23. A. M. ≥ G.M. : x3+2x3+4 ≥ 3∙3 2.24. A. M. ≥ G.M.: By 2.1. 2.25.Assume that a ≥ b ≥ c A.M. 2.26. By A. M. ≥ G.M. : Sn+n=(1+1)+(
2.27. By A. M. ≥ G.M. : a+ b+ ð a+b+4 2.28. By A. M. ≥ G.M.: an-1+an-2+…+a+1 ≥ n∙n Multiply both sides by a-1, then an-1 ≥ n∙(a-1) 2.29. Similarly
2.30. a,b,k,n>0; ab>ka+nb ⇒ a- n > a-n+b-k > 2.31. I-way. A. M. ≥ H.M.: [(a+b)+(b+c)+(c+a)]∙
⇔ II- way: By 2.1.and 1.4.:
2.32.By 1.37.
2.33. Similarly: b= 2.34. x+y=2-z; x2+y2=2-z2; by Cauchy’s inequality (x+y)2 ≤ (x2+y2)(12+12) ⇒ (2-z)2 ≤ 2(2-z2) ⇒ z(3z-4) ≤ 0 ⇒ 0 ≤ z ≤ 2.35. By 2.1.: 2.36. By 2.1. and 1.3.:
2.37. The given inequality is equivalent to
By Cauchy’s inequality and A. M. ≥ G.M.: (12+12+12)
A. M. ≥ G.M.: 2.38. By 2.1. and A. M. ≥ G.M.: = 2.39. =n(1+2+…+n) = By A.M
| ||
| <== previous page | | | next page ==> |
| Royalty free stock image and video options | | | Me: I’m fine. Woods is my boss. No big deal. |

 then
then 

 and m
and m  k >0 then
k >0 then
 Let
Let  be any real numbers, then
be any real numbers, then 
 2
2 
 then
then
 ,
, 

 If
If  ,
,  ,
, 

 If
If  , then
, then
 For
For



 ) a2+b2
) a2+b2 

 + bc + ca
+ bc + ca 3(
3(  + bc + ca)
+ bc + ca) ) a2+b2+c2
) a2+b2+c2 
 )
) 


 ab + bc + ca ≤ 1
ab + bc + ca ≤ 1 N and n>1)
N and n>1) 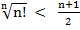

 ≥
≥  ∙ abc
∙ abc
 ≤ 4
≤ 4 
 (a,b,c
(a,b,c 


 a2+b2+c2
a2+b2+c2 


 a+b+c+abc
a+b+c+abc 
 ad < bc
ad < bc


 2 (ab+bc+ca)
2 (ab+bc+ca) 2
2

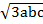
 )
) 
 )
) 
 )
) 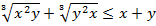




 )
)
 2(ab+bc+ca)
2(ab+bc+ca)


 4(a - d)
4(a - d) )
) 

 )
)  (1+2
(1+2  )
)  (1+2
(1+2  )
) 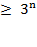

 ) (1+x)n
) (1+x)n 
 )(
)(  )
) 

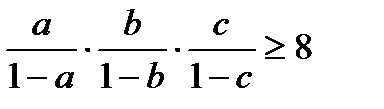

 )
)  +
+ 


 +
+  +
+ 



 +
+  +
+ 

 ) 3x3-6x2+4
) 3x3-6x2+4 

 abc(a+b+c)
abc(a+b+c) ) n
) n 

 an-1 ≥ n∙
an-1 ≥ n∙ 
 +
+ 
 ≤
≤ 
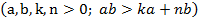 a+b >
a+b > 


 abc
abc 
 Find maximum and minimum values of z.
Find maximum and minimum values of z.

 ≥
≥ 









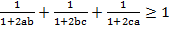




 (1-a)(1-b)(1-c)
(1-a)(1-b)(1-c) 






 x2+yz
x2+yz  2, y2+zx
2, y2+zx  2, z2+xy
2, z2+xy 





 a2+b2
a2+b2  a+b
a+b  ⇔ a2+b2 +c2
⇔ a2+b2 +c2 
 G.M. :
G.M. :  ,
, 


 ⇔
⇔ 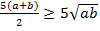 ;
;  ⇔
⇔  ;
;  ⇔
⇔  ⇒
⇒
 ⇒
⇒ 

 ⇒
⇒ 
 ⇒ Add them side by side.
⇒ Add them side by side.
 a2+b2+c2+14 ≥ 2(a+2b+3c)
a2+b2+c2+14 ≥ 2(a+2b+3c) ≥ 4 ∙ 4
≥ 4 ∙ 4  =
=  2 ≤ ≤(12+12+12+12)∙(a+b+c+d)=4∙8=32 ⇒
2 ≤ ≤(12+12+12+12)∙(a+b+c+d)=4∙8=32 ⇒  ∙2y)2 ≤ (22+
∙2y)2 ≤ (22+ 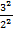 )(x2+4y2)=
)(x2+4y2)=  ⇒
⇒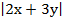 ≤
≤  ⇒
⇒  ∙
∙ 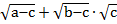 )2 ≤ (
)2 ≤ (  )(
)(  ) = ab
) = ab )2 ≤ ≤(12+12+12)(
)2 ≤ ≤(12+12+12)(  +
+  ) =3∙(4(a+b+c)+3)=3∙7=21
) =3∙(4(a+b+c)+3)=3∙7=21 =3∙
=3∙  abc ≤ 1. Then a+b+c+abc ≤ 3+1=4
abc ≤ 1. Then a+b+c+abc ≤ 3+1=4 ⇒
⇒  =
=  <
<
 , 2
, 2  ,
, <
<  …, 50
…, 50 
 +
+  +…+
+…+  >
>  2009∙
2009∙  =
=  .
. . Then given inequality is equivalent to
. Then given inequality is equivalent to ; Let’s prove it.
; Let’s prove it. 

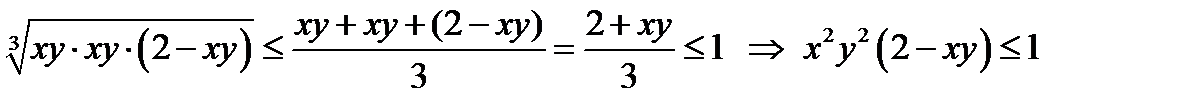




 and
and  ⇒
⇒ 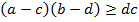 ⇒
⇒
 ⇔
⇔ ⇒
⇒ 
 ,
,  ⇒
⇒
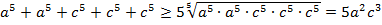
 ⇒
⇒
 G.M. :
G.M. : 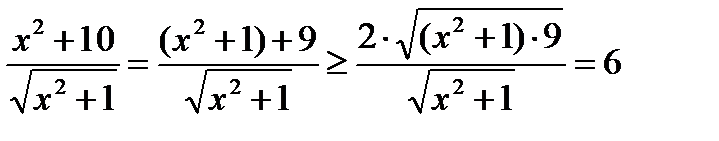
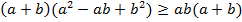 ⇔
⇔ ⇔
⇔ 

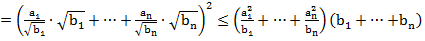
 ⇔
⇔ ; . A.M.
; . A.M. 



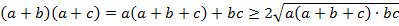
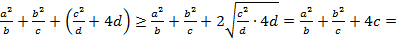
 ⇒
⇒ ⇔
⇔ 
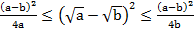
 ⇔
⇔  ⇔
⇔ ⇔
⇔ 
 ,
,  , …,
, …, ⇒
⇒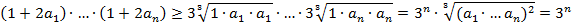
 =
= ⇒
⇒  , Similarly
, Similarly ; Multiply them side by side , then
; Multiply them side by side , then 
 then
then 
 , then by A.M.
, then by A.M. 
 ⇒
⇒ 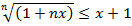 ⇒ (1+x)n
⇒ (1+x)n  ⇒
⇒ ⇒
⇒  Similarly
Similarly ;
; 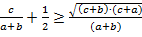 Multiply them side by side.
Multiply them side by side.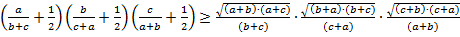 =1
=1
 .
.  :
: 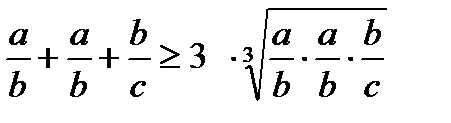
 ⇒
⇒  , Similarly:
, Similarly: 
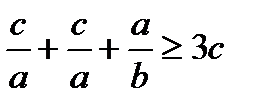 ⇒
⇒ +
+  +
+  3a+3b+3c ⇒
3a+3b+3c ⇒ 



 . It is 1.6.
. It is 1.6.
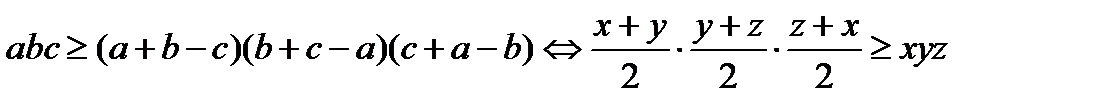 It is 1.6.
It is 1.6.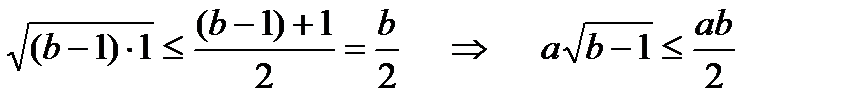
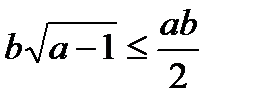 .
.  +
+ 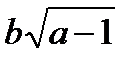




 +
+  +
+ 
 +
+  +
+  = 2
= 2 , But it is impossible .
, But it is impossible . Similarly
Similarly 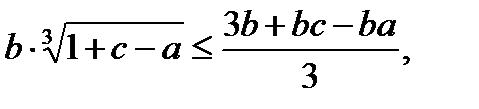

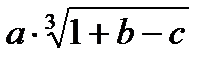 +
+ 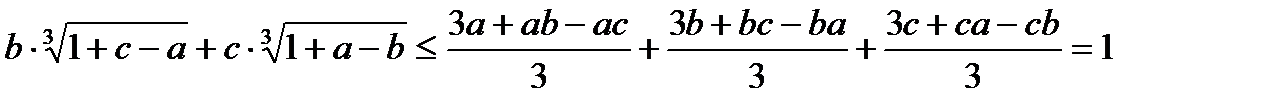
 xyz = 1,
xyz = 1, 

 Let’s prove it.
Let’s prove it. 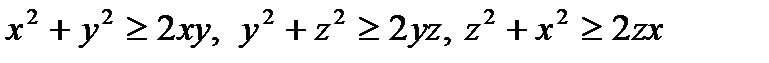
 . A.M.
. A.M.  G.M.:
G.M.:  Similarly
Similarly  ⇒
⇒ )+(
)+(  )+(
)+(  )
)  ⇒
⇒  (1)
(1) GM:
GM:  (2)
(2) +
+ 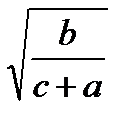 +
+  >2 Is 2.17. . After substitutions a=x2, b=y2, c=1
>2 Is 2.17. . After substitutions a=x2, b=y2, c=1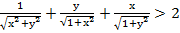
 G.M. :
G.M. :  ,
, . Add them side by side,then
. Add them side by side,then  .
. 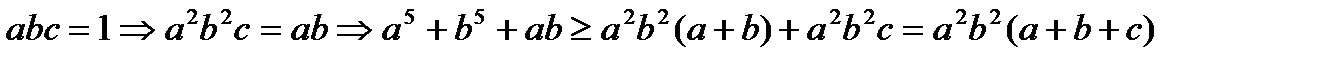
 ⇒
⇒ 

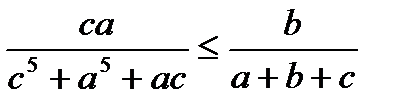 .
.



 = 6x2
= 6x2
 =
=  ⇒ ab
⇒ ab  ⇒
⇒  ≥ 4
≥ 4 +
+ 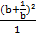 ≥
≥  =
=  ≥
≥  =
= 
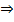 a3 ≥ b3 ≥ c3. By Chebyshev¢s inequality and
a3 ≥ b3 ≥ c3. By Chebyshev¢s inequality and
 ∙
∙ 
 =
= 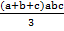
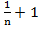 )=2+
)=2+  + … +
+ … +  ≥
≥ = n∙
= n∙ 
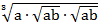 = 3∙
= 3∙ 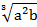 ,
,  = 3∙
= 3∙  ⇒
⇒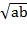 ≥ 3(
≥ 3(  ) is equivalent to the given inequality
) is equivalent to the given inequality = =n∙n
= =n∙n  = n∙n
= n∙n  = n∙
= n∙ 
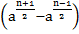
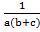 =
=  =
=  ≤
≤  is true by A. M. ≥ H.M.
is true by A. M. ≥ H.M. ,
,  ≤
≤  . Then
. Then
 > 0; b-k >
> 0; b-k >  > 0 ⇒
> 0 ⇒ = 2
= 2  ⇒ a-n+b- k >2
⇒ a-n+b- k >2  ≥ 9 ó
≥ 9 ó ≥
≥  ó (
ó ( 
 .
.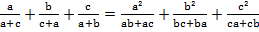 ≥
≥ 


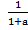 =x;
=x;  =y;
=y;  =z ⇒ x+y+z=1; a=
=z ⇒ x+y+z=1; a=  =
=  ;
; ; c=
; c=  ; By 1.6. abc =
; By 1.6. abc =  ≥ 8
≥ 8 ≥
≥  ≥
≥  =1
=1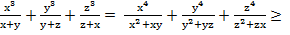
 ≥
≥ 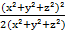 =
=  ≥
≥  ≥
≥ 
 ≥
≥  2=
2=  ∙
∙  ∙3∙ 3
∙3∙ 3  = 3
= 3  ≥
≥  ;
; ≥ 3. Then
≥ 3. Then  =
=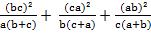 ≥
≥  =
=  ≥
≥  =
= 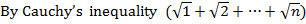 2
2  (
(  )(1+2+…+n)=
)(1+2+…+n)= . ⇒
. ⇒  .
. (
(  +
+  )
)  (
( 
 (
(