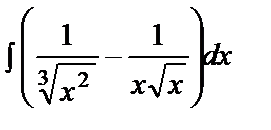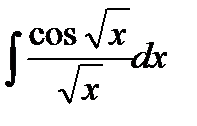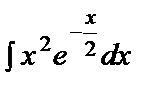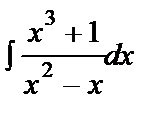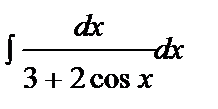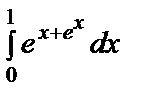CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
What is the Parabola?The focus, directrix of the parabola. Find equation of a line equidistant from the point À(2; 1) and a line x=0.
26. Sets. Operations with sets. The numeric set. Let
27. The concept of the function. The event and odd functions. Roundedness function. Find out even (odd) function
28. Monotonicity functions. Inverse function. Find the inverse of this function
29. Given a graph of the function y = f (x). Describe how to construct a graph of the following functions: y=f(õ)+b, y=f(õ+à), y=|f(õ)| . Draw the graph of the function ó = -x2+2x-3 and graphics above cases.
30. Given a graph of the function y = f (x). Describe how to construct a graph of the following functions: y=kf(õ), y=f(kõ), y=f(|õ|) . Draw the graph of the function ó = -x2+2x+3 and graphics above cases.
31. Given a graph of the function y = f (x). Describe how to construct a graph of the following functions: y=-f(õ), y=f(-õ), y=f(|õ|) . Draw the graph of the function ó = -x2-2x+3 and graphics above cases.
32. Limes of functions. Its properties. Calculate the limit of function
33. The first remarkable limit. Its consequence. Calculate the limit
34. The second remarkable limit. Its consequence. Calculate the limit
35. Infinitely small and infinitely large functions. Communication between the infinitely small and infinitely large functions. When the function And when the infinite?
36. Continuity of function y = f (x) at the point õ0. Formulate properties of continuous functions at a point.
37. One-Sided Limits. Find the one-side limits
38. Discontinuity of the first kind. Investigate for continuity function
39. Discontinuity of the second kind. Investigate for continuity function
40. Derivatives of Functions. The geometric Interpretation of the Derivative. Prove that
41. Differentiations Rules. Find the derivative
42. The Rolle Theorem. The geometric Interpretation. If
43. The L'Hopital Rule. Find the limit
44. Increasing and Decreasing Functions. Maxima and Minima of Functions. Find extremes of the function
45. Curvature of Functions. Find the inflection point and the intervals of convexity of the curve
46. Indefinite Integrals. Its properties. Evaluate the integral
47. Integration by Substitution. Evaluate the integral
48. Integration by Parts. Evaluate the integral
49. Integration of Rational Functions. Evaluate the integral
50. Integration of Trigonometric Functions. Evaluate the integral
51. The definite Integral. Its properties. Evaluate the integral
Date: 2015-04-20; view: 2488
|
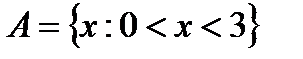 and
and 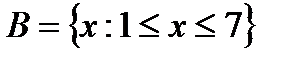 are numeric sets. Find the union, intersection, and difference (B\A) of them.
are numeric sets. Find the union, intersection, and difference (B\A) of them.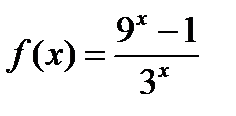 .
.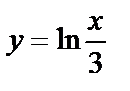 . Construct the graphs given and inverse functions.
. Construct the graphs given and inverse functions. as
as 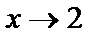 and
and 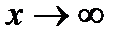 .
.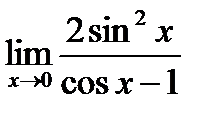 .
.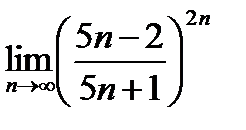 .
.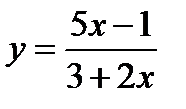 is infinitely small?
is infinitely small?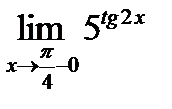 and
and 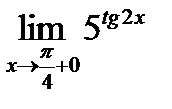 .
.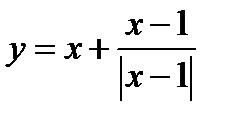 .
. .
.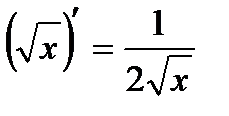 .
.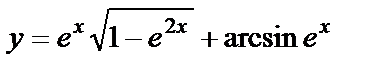
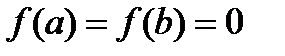 , as it is possible to formulate Rolle's theorem?
, as it is possible to formulate Rolle's theorem?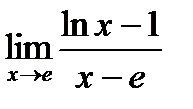
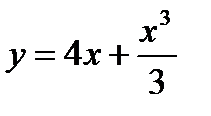 .
.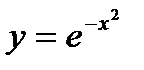 (Gaussian curve).
(Gaussian curve).