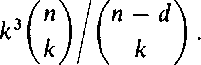Coding Theory

Consider a situation where errors are likely to occur in the transmission of information. Noise in the information channel might be due to technical failures or negligence on the part of the sender or receiver. In coding theory it is assumed that errors occur randomly and independently. It is equally likely for the bit 0 to be incorrectly received as the bit 1, as for the bit 1 to be incorrectly received as the bit 0. In this basic setup there is no malicious adversary acting on purpose. The purpose of coding theory is to introduce redundance in such a way that even if errors occur in the transmission, the received message can still be correctly interpreted. Of course, some assumption has to be made concerning the number of errors; no amount of redundancy is sufficient to correct unboundedly many errors.

More specifically, assume that d errors may occur in the transmission of a word w consisting of n bits. Thus, the received word w' differs from w with respect to at most d bits but the incorrect bits may occur anywhere in the word. Let C = {a,,.. ., a*} be a set of n-bit words a, such that any two of the a's differ with respect to at least 2d + 1 bits. Then C is referred to as a d-error correcting code. Indeed, a, can be correctly inferred from the received cl\, since a, and a\ differ with respect to at most d bits, whereas aj differs from any a.j.j ^ i, with respect to at least d + 1 bits.

Although decoding, that is recovering a_; from al, is always possible in principle, it might still be intractable computationally. In fact, the public-key cryptosystem described below uses the idea that the public-key leads to an intractable decoding problem, whereas the trapdoor enables the receiver to decode easily.

Thus, coding theory and cryptography have opposite aims. In coding theory one tries to write the message in such a form that reasonably many errors can be tolerated in the transmission. In this sense the clarity of the message is increased. In cryptography, on the other hand, one tries to decrease the clarity in order to make the message incomprehensible for an eavesdropper. Because of these opposite aims it is difficult to combine the two approaches, although it would be very important to translate messages into a form protected both against eavesdroppers and random noise. For this purpose, the message should first be encrypted, after which
an error correcting code should be applied to the result. A reverse order of these two operations is not meaningful for obvious reasons. Protection against both noise and an active eavesdropper seems to be impossible. Altogether the details of combining cryptography with coding theory are not yet properly understood.

Such a combination is not intended in the public-key cryptosystem described briefly below. The system is due to McEliece and resembles knapsack systems, in particular, the ones based on dense knapsacks. The cryptosystem uses d-error correcting Goppa codes. Such a code {a,, . . . ,a_t} is based on a polynomial of degree d irreducible over the finite field F(2^m). It can be represented in terms of a binary k x n generator matrix M, where n = 2^m. The cryptosystem designer chooses arbitrary binary matrices S and P such that S is a nonsingular k x k matrix and Panuxn permutation matrix. The product M' = SMP is understood as a binary matrix, where all numbers are reduced modulo 2.

The crucial fact is that M' at least looks like the generator matrix for an arbitrary linear code. No tractable decoding algorithms are known for linear codes, whereas Goppa codes are easy to handle.

The cryptosystem designer publicizes M' as the encryption key but keeps S, M and P as the secret trapdoor. From the trapdoor information also the inverses and P^_1 can be immediately computed.

A plaintext block w consisting of k bits is encrypted as

c = wM' © b ,

where b is an arbitrary binary n-dimensional vector with exactly d components equal to 1 and © denotes bitwise addition. Vectors b are chosen by the sender separately for each block w.

The legal receiver knows that M' = SMP and computes

cP~^l = wSM © ftP^-1 .

Since P is a permutation matrix, exactly d components of bP'¹ equal 1. Hence, the error vector bP~^x can be removed by the decoding technique of Goppa codes, yielding wS. From this w is immediately recovered by multiplying with S~^!.

An eavesdropper faces the problem of decoding an apparently linear code. Decoding for linear codes is an /VP-complete problem.

Cryptanalysis by preprocessing appears hopeless if n and d are large enough: there are too many possibilities for M, S and P. For instance, if n = 1024 and d = 50 there are approximately 10¹⁴⁹ possible polynomials that can be used as a basis for a Goppa code. The parameters are tied by the formula k = 2^m — md = n — md. Assuming that the inversion of a k x k matrix requires k³ steps, the time complexity of brute force cryptanalysis by preprocessing can be estimated as

Date: 2015-02-16; view: 715